Ez az oldal a háromdimenziós vagy “szilárd” alakzatok tulajdonságait vizsgálja.
egy kétdimenziós alaknak hossza és szélessége van. A háromdimenziós szilárd alaknak mélysége is van. A háromdimenziós alakzatoknak természetüknél fogva van egy belső és egy külső, amelyet egy felület választ el egymástól. Minden fizikai elem, amit megérinthet, háromdimenziós.,
Ez az oldal kiterjed mind az egyenes oldalú, poliédereknek nevezett szilárd anyagokra, amelyek sokszögeken alapulnak, mind a görbékkel rendelkező szilárd anyagokra, például gömbökre, hengerekre és kúpokra.
poliéderek
a poliéderek (vagy poliéderek) egyenes oldalú szilárd formák. A poliéderek poligonokon alapulnak, két dimenziós sík alakú, egyenes vonalakkal.
tekintse meg oldalunkat a sokszögek tulajdonságai a sokszögekkel való együttműködésről.
a poliéderek a következők:
- egyenes élek.
- lapos oldalak úgynevezett arcok.,
- sarkok, úgynevezett csúcsok.
a Poliédereket gyakran az éleik, arcaik és csúcsaik száma határozza meg, valamint az, hogy arcuk azonos alakú és méretű-e. A poligonokhoz hasonlóan a poliéderek is lehetnek szabályosak (szabályos sokszögek alapján) vagy szabálytalanok (szabálytalan sokszögek alapján). A poliéderek homorúak vagy konvexek is lehetnek.
az egyik legalapvetőbb és legismertebb poliéder a kocka. A kocka egy szabályos poliéder, amelynek hat négyzet alakú felülete, 12 széle és nyolc csúcsa van.,

szabályos Polihedronok (platonikus szilárd anyagok)
az öt szabályos szilárd anyag a polihedronok egy speciális osztálya, amelyek mindegyik arca azonos azzal, hogy minden arca szabályos sokszög. A platonikus szilárd anyagok a következők:
- tetraéder négy egyenlő oldalú háromszög arccal.
- kocka hat négyzet alakú arccal.
- nyolc egyenlő oldalú háromszög alakú oktaéder.
- dodekaéder tizenkét pentagon arccal.
- ikozaéder húsz egyenlő oldalú háromszög arccal.,
lásd a fenti ábrát a rendszeres poliéderek mindegyikének illusztrációjához.
mi az a Prizma?
a prizma bármely poliéder, amelynek két egyforma vége és lapos oldala van. Ha a prizmát bárhol a hossza mentén vágja le, a végével párhuzamosan, keresztmetszete ugyanaz – két prizmával végződne. A prizma oldalai párhuzamosak-négyoldalas formák, két azonos hosszúságú oldalpárral.
az Antiprizmák hasonlóak a rendszeres prizmákhoz, végeik megegyeznek., Az anti-prizmák oldalai azonban háromszögekből állnak, nem pedig parallelogrammokból. Az antiprizmák nagyon összetettekké válhatnak.
mi a piramis?
a piramis egy sokszög alapú poliéder, amely egyenes oldalú csúcshoz (csúcsponthoz) kapcsolódik.
bár hajlamosak vagyunk a négyzet alapú piramisokra gondolni, mint amilyeneket az ókori egyiptomiak építettek, valójában bármilyen sokszög alapúak lehetnek, szabályosak vagy szabálytalanok. Továbbá, egy piramis lehet egy csúcsa a közvetlen közepén a bázis, a jobb piramis, vagy lehet a csúcs off központ, Ha ez egy ferde piramis.,
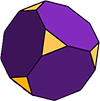
összetettebb poliéderek
a poliédernek több típusa létezik: szimmetrikus és aszimmetrikus, konkáv és konvex.
például az Archimedean szilárd anyagok legalább két különböző szabályos sokszögből állnak.
a csonka kocka (az ábrán látható) egy Archimedean szilárd, 14 arccal. Az arcok közül 6 szabályos oktagon, a másik 8 szabályos (egyenlő oldalú) háromszög. Az alaknak 36 széle és 24 csúcsa van (sarkok).,
háromdimenziós formák görbékkel
szilárd formák, amelyek ívelt vagy kerek éleket tartalmaznak, nem poliéderek. A poliéderek csak egyenes oldalúak lehetnek.
a körülötted lévő objektumok közül sok legalább néhány görbét tartalmaz. A geometriában a leggyakoribb ívelt szilárd anyagok a hengerek, kúpok, gömbök és tori (a tórusz többes száma).,
| Közös Háromdimenziós Formák Görbék: | |
|---|---|
| Henger | Kúp |
 |
 |
| Egy henger azonos keresztmetszet egyik végétől a másikig. A hengereknek két azonos vége van egy körnek vagy oválisnak. Bár hasonló, a hengerek nem prizmák, mivel a prizmának (definíció szerint) paralelogramma, lapos oldala van., | a kúpnak kör alakú vagy ovális alapja és csúcsa (vagy csúcsa) van. A kúp oldala simán tapad a csúcsra. A kúp hasonlít egy piramishoz, de különbözik attól, hogy a kúpnak egyetlen ívelt oldala és egy kör alakú alapja van. |
| Sphere | Torus |
 |
 |
| a gömb alakú gömb egy teljesen gömb alakú gömb kerek tárgy. A gömb felszínének minden pontja egyenlő távolságra van a gömb középpontjától., | gyűrű, gumiabroncs vagy fánk alakú, szabályos gyűrűs torus alakul ki egy kisebb kör körül egy nagyobb kör körül. A tori összetettebb formája is van. |
felület
a számítási területről szóló oldalunk elmagyarázza, hogyan kell kidolgozni a kétdimenziós formák területét, és meg kell értenie ezeket az alapokat a háromdimenziós formák felületének kiszámításához.
a háromdimenziós formák esetében a felületről beszélünk, hogy elkerüljük a zavart.,
a kétdimenziós formák területével kapcsolatos ismereteit felhasználhatja egy háromdimenziós alak felületének kiszámításához, mivel minden arc vagy oldal ténylegesen kétdimenziós alak.
ezért kidolgozza az egyes arcok területét, majd összeadja őket.
mint a lapos formák esetében, a szilárd anyag felületét négyzet egységekben fejezzük ki: cm2, inches2, m2 stb. A mértékegységekről részletesebben az oldalunkon található mérési rendszerek.,
példák felületi számítások
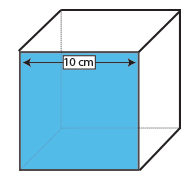
Cube
a felület egy kocka a terület egy arc (Hossz x szélesség) szorozva 6, Mert mind a hat arc ugyanaz.
mivel egy kocka arca egy négyzet, csak egy mérést kell elvégeznie – a négyzet hossza és szélessége definíció szerint azonos.
ennek a kockának az egyik oldala tehát 10 × 10 cm = 100cm2. Szorozzuk meg 6-tal, az arcok számát egy kockán, és azt találjuk, hogy ennek a kockának a felülete 600cm2.,
Egyéb szabályos poliéderek
Hasonlóképpen a többi szabályos poliéder (platonikus szilárd anyag) felülete kidolgozható az egyik oldal területének megtalálásával, majd a választ megszorozva az oldalak teljes számával – lásd a fenti alapvető poliéderek ábráját.
Ha egy dodekaédert alkotó pentagon területe 22cm2, akkor szorozza meg ezt az oldalak teljes számával (12), hogy megadja a választ 264cm2.,
piramis
egy standard piramis felületének kiszámításához négy egyenlő háromszög alakú oldallal és négyzet alappal:
először dolgozza ki az alap (négyzet) hosszának × szélességének területét.
ezután dolgozza ki az egyik oldal területét (háromszög). Mérje meg a szélességet az alap mentén, majd a háromszög magasságát (más néven ferde hossz) az alap központi pontjától a csúcsig.,
ezután megoszthatja a választ 2-vel, hogy megadja egy háromszög felületét, majd szorozza meg 4-gyel, hogy mind a négy oldal felületét megkapja, vagy egyszerűen szorozza meg egy háromszög felületét 2-vel.
végül adja hozzá a bázis és az oldalak területét, hogy megtalálja a piramis teljes felületét.
más típusú piramisok felületének kiszámításához össze kell adni az alapterületet (az úgynevezett alapterületet) és az oldalak területét (oldalsó területet), előfordulhat, hogy az oldalakat egyedileg kell mérni.,
nettó diagramok
a geometriai háló egy háromdimenziós objektum kétdimenziós “mintája”. A hálók hasznosak lehetnek egy háromdimenziós tárgy felületének kidolgozásakor. Az alábbi ábrán látható, hogy az alapvető piramisok hogyan épülnek fel, ha a piramis “kibontakozik”, akkor a hálóval marad.
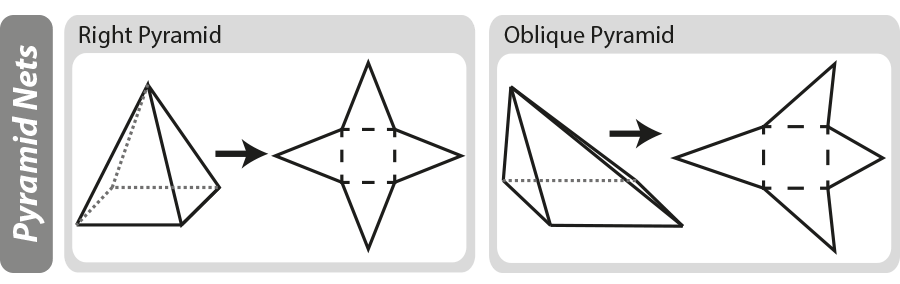
További információ a net diagramokról lásd oldalunkat 3D alakzatok és hálók.

Prism
egy prizma felületének kiszámításához:
a Prizmáknak két vége van, azonos és lapos parallelogramm oldalakkal.,
Számítsa ki az egyik vég területét, majd szorozza meg 2-vel.
egy szabályos prizmához (ahol minden oldal azonos) számítsa ki az egyik oldal területét, majd szorozza meg az oldalak teljes számát.
szabálytalan prizmák esetén (különböző oldalakkal) kiszámítja az egyes oldalak területét.
adja hozzá a két választ (végek × oldalak), hogy megtalálja a prizma teljes felületét.,
henger

példa:
sugár = 5cm
magasság = 10cm
a henger felületének kiszámításához hasznos az alakzat alkatrészeire gondolni. Képzeljünk el egy ón csemegekukorica-van egy felső és egy alsó, mindkettő körök. Ha az oldalt hosszában levágjuk, és ellapítjuk, akkor téglalapot kapunk. Ezért meg kell találni a terület két kört, majd egy téglalapot.
először dolgozza ki az egyik kör területét.
a kör területe π (pi) × radius2.,
5cm sugarú körben az egyik kör területe 3,14 × 52 = 78,5cm2.
szorozzuk meg a választ 2-vel, mivel két kör van 157cm2
a henger oldalának területe a kör kerülete × a henger magassága.
kerülete egyenlő π x 2 × sugárral. Példánkban, 3.14 × 2 × 5 = 31.4
mérje meg a henger magasságát – ebben a példában a magasság 10 cm. Az oldal felülete 31,4 × 10 = 314cm2.,
A teljes felület megtalálható hozzáadásával a terület a körök, valamint az oldalon együtt:
157 + 314 = 471cm2

Példa:
Radius = 5cm
Hossza Ferde = 10cm
Kúp
kiszámításakor a felülete kúp kell használni a hossza a ‘ferde’, valamint a sugara a bázis.
azonban viszonylag egyszerű kiszámítani:
a kör területe a kúp alján, π (pi) × radius2.
ebben a példában az összeg 3.14 × 52 = 3.14 × 25 = 78.,5cm2
az oldal területe, a lejtős szakasz, a következő képlet segítségével található:
π (pi) × sugara × ferde hossza.
példánkban az összeg 3,14 × 5 × 10 = 157cm2.
végül adja hozzá az alapterületet az oldalsó területhez, hogy megkapja a kúp teljes felületét.
78,5 + 157 = 235.5cm2

teniszlabda:
átmérő = 2,6 hüvelyk
gömb
a gömb felülete egy kör területének képletének viszonylag egyszerű kiterjesztése.
4 × π × radius2.,
egy gömb esetében gyakran könnyebb mérni az átmérőt-a gömbön keresztüli távolságot. Ezután megtalálhatja azt a sugarat, amely az átmérő fele.
a standard teniszlabda átmérője 2,6 hüvelyk. A sugár tehát 1,3 hüvelyk. A képlethez szükségünk van a sugár négyzetére. 1.3 × 1.3 = 1.69.
a teniszlabda felülete tehát:
4 × 3, 14 × 1, 69 = 21, 2264 inches2.,

példa:
R (nagy sugár) = 20 cm
r (kis sugár) = 4 cm
Torus
a torus felületének kiszámításához két sugárértéket kell találnia.
a nagy vagy nagy sugarat (R) a lyuk közepétől a gyűrű közepéig mérjük.
a kis vagy kisebb sugarat (r) a gyűrű közepétől a külső szélig mérjük.
az ábra egy példa tórusz két nézetét mutatja, valamint a sugarak (vagy sugarak) mérésének módját.,
a felület megtalálásához szükséges számítás két részből áll (mindegyik sugár esetében egy). A számítás minden egyes résznél azonos.
a képlet a következő: surface area = (2NR) (2nr)
a példa tórusz felületének kidolgozásához.
(2 × π × R) = (2 × 3.14 × 20) = 125.6
(2 × π × r) = (2 × 3.14 × 4) = 25.12
szorozzuk össze a két választ, hogy megtaláljuk a példa tórusz teljes felületét.