Calculate Log & Antilog Online (Magyar)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

ahol,

• b = alap,
• y = szám,
• x = log érték.

Antilog kiszámítása:

y = 10x

ahol

• x = szám,
• y = antilog érték.

a Logaritmus, valamint Anti-Logaritmus: Hogyan Működik, illetve Ennek Jelentőségét

– Kézikönyv Szerzője által Corin B. Arenas közzétett, október 1-jén, 2019

Ha valaha is azon, hogy a szakértők meghatározni, nagy távolságok, földrengés intenzitása, valamint a globális gazdasági növekedési ütem, akkor jöttem, hogy jó helyen jár.

a nagyon nagy összegek kiszámítása lassú és zavaró lehet., De a logaritmus (log) és antilogaritmus (antilog) segítségével a számítások egyszerűbbek lehetnek.

Olvass tovább, hogy többet megtudj a naplóról és az antilogról, hogyan működnek, és hogy ezek miért releváns matematikai fogalmak.

mi a logaritmus?

a logaritmus az a teljesítmény, amelyre egy számot (amelyet bázisnak neveznek) meg kell szorozni magának egy adott szám megszerzéséhez. Egyszerűbb értelemben a logaritmus megoldja a problémát:

hányszor szorozzuk meg a b-t, hogy újabb y számot kapjunk?,

logaritmus számít hányszor ugyanazt a tényezőt meg kell szorozni, hogy érkezik egy adott számot.

ki találta ki?

a naplót a 16.században találták ki számítási eszközként John Napier skót matematikus, fizikus és csillagász. A Mirifici Logarithmorum Canonis Descriptio című könyvet a természetes logaritmusokat tárgyaló táblázatokkal és számokkal írta, megalapozva annak alapkoncepcióját.

Napier a logaritmus kifejezést a görög Logosz szóból alkotta meg, ami azt jelenti, hogy “Arány vagy Arány”, és arithmos, ami azt jelenti, hogy ” Szám.,”Ha együtt, szó szerint azt jelenti,” Arány száma.”

2 típusú logaritmusok

egy szám természetes logaritmusa az e konstans alapjához tartozó naplója, ahol e megközelítőleg egyenlő a 2.718281828459 értékkel. Az egyenletet lobe(x) alakban írják.

Ha egy logaritmus nem határoz meg egy bázist, mint például: log (1000), akkor ez egy közös logaritmus, amely az alap 10-et használja.

log(1000), ez ismert, mint egy közös logaritmus, amely az alap 10.

hogyan használják a naplót?,

miután milliókkal, milliárdokkal kezdte meg a számadatok kiszámítását, elég megadóztatóvá válhat. Függetlenül attól, hogy sok pénzt számol, a népesség növekedése vagy a nagy távolságok lefedése, a napló működhet az Ön számára. Egyszerűsítheti a nagy összegeket, amelyek hosszú és zavaros egyenleteket tartalmaznak, megkönnyítve azok megértését.

itt van a log standard egyenlete:
logb (x) = y

ahol,

• a szám önmagához szorozva (b) az alap.
• a szorzatok száma (y) a logaritmus.,
• a kapott szám (x) zárójelben van írva.

ahhoz, hogy megértsük, hogyan működik a koncepció, itt van egy példa egy kisebb számmal:
kérdés: hány 2-et szorozunk, hogy 32-et kapjunk?
b = 2, x = 32

log2(32) = y
válasz: 2 x 2 x 2 x 2 x 2 = 32

5 a 2-es számot meg kell szorozni a 32-es szám megszerzéséhez.
a válasz: log2(32) = 5

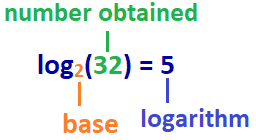
ezért ebben a példában: a 32 logaritmusa a 2 bázissal 5, vagy a 32 logaritmusa 5.,

ezenkívül a log az exponencia inverz függvénye, ahol a matematikai műveletet bn-ként írják. b az a bázis, amelyet az n erejének megfelelően megszoroznak, ami az a szám, amikor önmagához szorozzák.

mit jelent ez? Egy szám naplója az a kitevő, amelyhez a B bázist megszorozzuk egy adott szám megszerzéséhez. Ahhoz, hogy egy jobb ötlet, olvassa el a minta log egyenlet mellett az exponenciális egyenlet alatt.,

log
log2(32) = 5	25 = 32

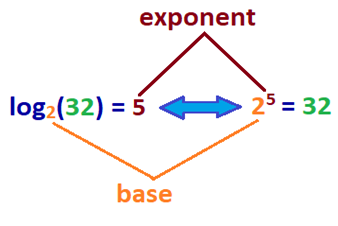
most próbáljuk meg nagy számmal.
Kérdés: hány 10s mi szaporodnak, hogy 150,000,000,000?
b = 10, x = 150,000,000,000

logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.,1760912590557

ezt egy tudományos számológép naplófunkciójának segítségével oldják meg. Vagy használja a számológépet ezen az oldalon, hogy megkapja a választ.

hogyan kapcsolódik az Antilogaritmus a naplóhoz?

egy naplószám ezután visszaadható az eredeti számra. Ezt antilogaritm (antilog) segítségével lehet elvégezni. Így az antilog a log inverz funkciója. Hasonlóképpen, az antilog egy egyszerűsített naplóérték exponencializálására szolgál.,

az Y szám antilogjának kiszámításához fel kell emelnie a B logaritmusbázist (általában 10, néha az állandó e) az y szám generálására.

itt van az antilog egyenlete a 10 bázis használatával:
10x = y
ahol x az exponens, y pedig az antilog érték.

például, ha ezt az egyenletet vesszük, log(5) = x, antilogja 10x = 5 lesz.

• Log: log(5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

most próbáljuk meg nagyobb számmal.,

Ha vesszük log(150,000,000,000) = x, a antilog lesz 10x = 150,000,000,000.

• Napló: log10(150,000,000,000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150,000,000,000

Fontos, de Valós Alkalmazások

Előtt, hogy a találmány számológépek, logaritmus használták számítások egyszerűsítése, a különböző területeken, a tudás, mint például a navigációs, földmérési, csillagászat, majd később a mérnöki.

képzelje el a vitorlázást a semmi közepén a 16.században., A navigátorok akkoriban a csillagok helyzetére és egy szextáns mechanizmusra támaszkodtak, hogy pontosan meghatározzák a pontos helyüket. A modern technológia nélkül, amely segít nagy távolságok kiszámításában, a log segítségével egyszerűsítheti számításait. A pontosság fontos, vagy több napot kockáztat a tengeren, szűkös készletekkel. Kevesebb egyenlet azt jelenti, kevesebb helyet hiba.

mi a helyzet más gyakorlati alkalmazásokkal? Élő Tudomány Államok logaritmus kapcsolódnak geometriai progresszió aritmetikai progresszió., Ha valaha is észrevetted az ismétlődő formákat és mintákat a természetben, az építészetben és a művészetben, ezek a formációk saját logaritmikus értékekkel rendelkeznek.

ma a minták működésének ismerete befolyásolja azt, ahogyan az emberiség épít és tervez házakat, épületeket és városi tájakat.

a logaritmusokat bizonyos skálák mértékének és intenzitásának kifejezésére is használják., Eltekintve széles távolságok, majd nagy sebességgel, az intézkedések egyéb dolgok, mint például:

• Hang intenzitása
• Hang frekvencia
• Erő szélviharok
• erősségű földrengés
• Maró szintű savak
• ásványok Keménysége
• Fényerő a csillagok,

nézzük decibel példaként. Annak érdekében, hogy a hangszórók 10 decibellel hangosabbak legyenek, azt a teljesítmény 10-szeresével kell ellátni. Ahogy növeli azt +20 dB – re,100-szorosára lesz szüksége a teljesítménynek, +30 dB-vel pedig 1000-re lesz szüksége.

ráadásul a hang intenzitása aritmetikusan halad előre., Arányosan változik a geometriailag előrehaladó hanghullám logaritmusával is.

Az alábbiakban egy Élő Tudomány táblázata található, amely felsorolja a különböző logaritmikus skálákat a megfelelő lineáris skálákkal.

mérési sebességekben és rangsorokban

Kalid Azad szerint a matematikai oktató mögött BetterExplained.com, logaritmusok hogyan találjuk ki, milyen gyorsan növekszik valami.

a közös logaritmusok alapvetően a számokat írják le a 10-es hatáskörük szempontjából. Ami a kamatlábat illeti, a logaritmus egy befektetés növekedése.,

egy ország GDP-növekedési ütemének meghatározásakor az elemzők a következő években felülvizsgálják a GDP-t. Figyelembe veszik az előző év GDP-jét, a következő év GDP-jét, majd kiszámítják a logaritmust, hogy megtalálják a becsült növekedési rátát.

a keresőmotorok a hivatkozási grafikont használják, hogy segítsék a dokumentumok fontosságát, megbízhatóságát & az Interneten keresztül. A Google Pagerankja a Keresés egyik jelentős fejlődése volt, amely növelte a keresési relevanciát, és segített a Google search marketshare-nak.,

Azad szerint 1-10-es skálán a 2-es oldalas nyitóoldal 10-szer népszerűbb,mint egy 1-es oldalas oldal. Ha egy webhelynek 5-ös Pagerankja van, a versenytárs webhelynek pedig 9-es Pagerankja van, akkor 4 nagyságrendű különbséggel rendelkezik.

a nagyságrendje nagyjából 10x különbséget jelent, vagy a rangsor 1 számjegyű nagyobb a másikhoz képest. Ebben az esetben a PageRank 9 webhely 100 000 000 népszerűbb, mint a PageRank 1 webhely.,

az alsó sor

napló és antilog jelentős számítási módszerek, amelyek lehetővé teszik számunkra, hogy egyszerűsítse a nagy összegeket. Az egyszerűsítés lerövidíti a számítási folyamatot, és megkönnyíti a számítások megértését. Ez segít csökkenteni a hiba helyét.

továbbá a log használata mérhető skálákat biztosít a természeti jelenségek mérésére, mint például a földrengés intenzitása, a szélviharok ereje, valamint a csillagok fényereje. Pénzügyi szempontból a logaritmusok lehetővé teszik, hogy pontosan meghatározzuk a kamatlábakat és a gazdasági növekedési rátákat.

gyakorlatilag sok területen használják., A mérés pontosságától függő nagy értékek a logaritmikus számítások használatából származnak.

A szerzőről

Corin a pénzügyi témák lelkes kutatója és írója-tanulmányozza a gazdasági trendeket, hogyan befolyásolják a populációkat, valamint hogyan segíthet a fogyasztóknak bölcsebb pénzügyi döntések meghozatalában. Az ő más funkció cikkek is olvasható Inquirer.net és Manileno.com. a Fülöp-szigeteki Egyetemen, a világ egyik legjobb tudományos intézményében, Kreatív írásban mesterfokozatot szerzett, A Miriam College kommunikációs művészetében pedig főiskolai diplomát szerzett.