az adott parabolákhoz tartozó kvadratikus függvények megtalálása – kvadratikus függvények

az adott Parabolákhoz tartozó kvadratikus függvények megtalálása

olyan sok különböző típusú probléma merül fel a kvadratikus egyenletek tekintetében. Ebben a cikkben, a hangsúly kerül, hogyan tudjuk fejleszteni a másodfokú egyenlet egy másodfokú gráf segítségével egy pár különböző módszerekkel., De mielőtt belemennénk az ilyen típusú problémákba, szánjon egy percet arra, hogy Négyzetes kifejezésekkel játsszon ezen a csodálatos online grafikus számológépen. Minél kényelmesebb a kvadratikus grafikonok, kifejezések, annál könnyebb lesz ez a téma!

most menjünk bele a problémák megoldásába ezzel a tudással, nevezetesen, Hogyan találjuk meg a parabola egyenletét!

Hogyan találhatunk egy kvadratikus egyenletet egy grafikonból:

annak érdekében, hogy kvadratikus egyenletet találjunk egy grafikonból, két egyszerű módszer alkalmazható: 2 pont használatával vagy 3 pont használatával.,

1) Keresse meg a kvadratikus egyenletet 2 pontból

annak érdekében, hogy egy négyzetes egyenletet egy grafikonból csak 2 pontot használjon, az egyik pontnak a csúcsnak kell lennie. A csúcs és egy másik pont segítségével ezeket a koordinátákat a “vertex formának” nevezzük, majd megoldjuk az egyenletünket., A vertex képlet a következők szerint, amennyiben (d,f) a vertex pont (x,y) a másik ponthoz:

(y±d)=a(x±f)2(y \pm d) = a(x \pm f)^{2}(y±d)=a(x±f)2

Vertex formában is írt a több “igazi” formája, mint:

y=a(x±f)2∓dy = a(x \pm f)^{2} \mp dy=a(x±f)2∓d

ezzel a képlettel, annyit kell tenned, hogy al a vertex, a másik pont, oldja meg a, majd átírni az utolsó egyenlet., A legjobb módja annak, hogy kényelmessé váljon az űrlap használatával, ha példát mutat vele.

példa:

határozza meg az alábbi képen látható parabola egyenletét.

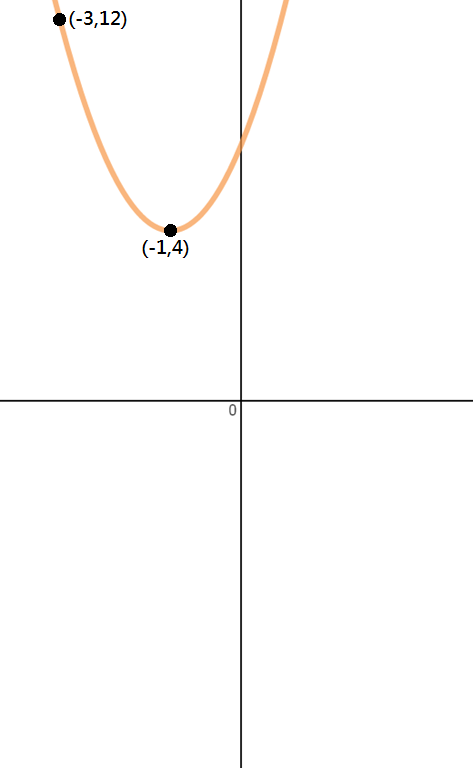
1.lépés: azonosítsa a pontokat

mivel csak két pontot kapunk ebben a probléma, a csúcs és egy másik pont, meg kell használni Vertex formában, hogy megoldja ezt a kérdést.,

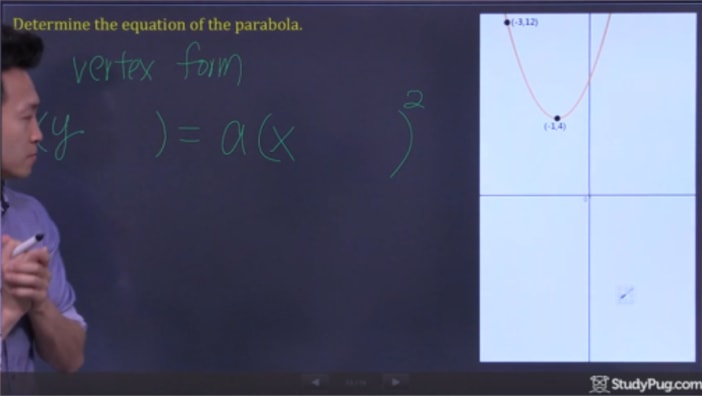
2. Lépés: Sub Pontot A Vertex Formában Megoldani az “a”

Most csak annyit kell tenned, hogy sub be a két pontot a vertex formula megoldani az “a”, hogy a szükséges adatokat írni a jogerős másodfokú egyenlet.,4)=egy(-3+1)2(12 – 4) = egy(-3 + 1)^{2}(12-4)=egy(-3+1)2

8=a(-2)28 = egy(-2)^{2}8=a(-2)28=4a8 = 4a8=4aa=2a = 2a=2

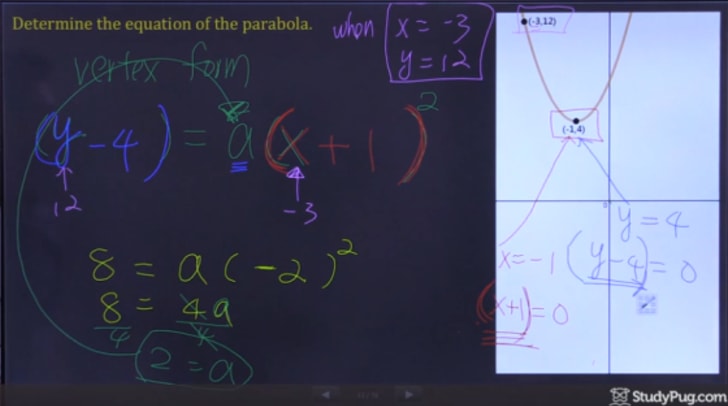
3. Lépés: Írd Ki Másodfokú Egyenlet

megoldása Után az “a” -, most már minden információt meg kell írni, ki a végleges választ.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

aztán, megfelelő csúcs formában a parabola, a végső válasz:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

, Hogy befejezi a leckét a vertex formában, hogyan találja meg egy másodfokú egyenlet a 2 pontot!, Ha frissíteni szeretné a memóriát a kapcsolódó témákban, például hogyan lehet megoldani a kvadratikus kifejezéseket vertex formában, hogyan lehet átalakítani egy szabályos kvadratikus egyenletet a standard űrlapról a csúcsformára a négyzet kitöltésével, és hogyan kell használni a vertex képletet, győződjön meg róla, hogy nézd meg a leckéket.

2) Keresse meg a kvadratikus egyenletet 3 pontból

egyes esetekben nem leszünk olyan szerencsések, hogy megkapjuk a pontot a csúcson. Ha ez a helyzet, akkor már nem találjuk meg a kvadratikus kifejezést mindössze két ponttal, és egy kicsit másképp kell csinálnunk., Abban az esetben, ha információt kapunk egy parabola x-elfogásáról, valamint egy másik pontról, akkor a kvadratikus egyenletet egy “faktorált formának”nevezett egyenlet segítségével találjuk meg. Az általános egyenlet a számításba formában képlet az alábbiak szerint történik, b, c, hogy az x-koordináta értékét az x-metszet:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

ezzel a képlettel, annyit kell tenned, hogy sub az x-koordinátáit az x-metszet, egy másik pont, majd oldja meg a szóval írhatunk ki a végleges választ., Ismét a legjobb módja annak, hogy kényelmesebbé tegyük a kvadratikus egyenletek ezen formáját, egy példaprobléma elvégzése.

Példa:

Meghatározni az egyenlet a parabola jelenik meg a kép alatt:

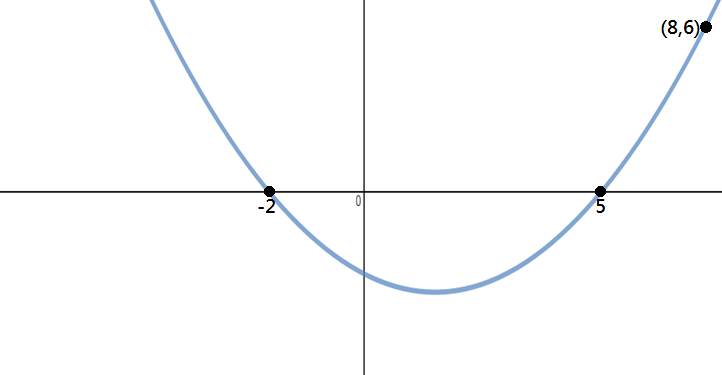
1. Lépés: Azonosítani Pontot

Mivel adott három pont ez a probléma, az x-metszet, a másik pont, használhatjuk számításba formában, hogy megoldja ezt a kérdést.,

a grafikonon látható, hogy az x-interceptorok -2 és 5, a parabola pontja pedig (8,6).

2. lépés: sub pontok Vertex formában megoldani ” a “

most már csak annyit kell tennünk, hogy sub értékeinket a faktorált formában képlet és megoldani az” a”, hogy az összes információt, hogy írjon a végső másodfokú egyenlet.,(x – 5)y=(x+2)(x−5)

a Következő használhatjuk a pont a parabola (8,6), hogy megoldja az “a”:

6=egy(8+2)(8-5)6 = egy(8 + 2)(8 – 5)6=a(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30aa=15a = \frac{1}{5}a=51

3. Lépés: Írd Ki Másodfokú Egyenlet

megoldása Után az “a” -, most már minden információt meg kell írni, ki a végleges választ.,

y=15(x+2)(x−5)y = \frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

Ez a két legfontosabb módszer egy adott parabola kvadratikus funkciójának megtalálására. További vizsgálat céljából a másodfokú függvények grafikonok, nézd meg ezeket a hasznos videók foglalkozik a diszkriminancia, grafikus, a másodfokú egyenlőtlenségek, valamint a kúpszeletek.