
egy rövid magyarázat és bizonyítás
a Rational Root Theorem (RRT) egy praktikus eszköz, hogy a matematikai arzenál. Ez biztosítja és gyors és piszkos teszt a racionalitás egyes kifejezések. Segít megtalálni a polinomok racionális gyökereit.,
itt van, hogyan és miért működik.,e53714″>
, Hogy A
Tegyük fel, hogy van egy polinom mértéke n, egész együtthatós:

A Racionális Root-Tétel kimondja, hogy: Ha egy racionális root létezik, akkor összetevői meg fogja osztani az első, valamint az utolsó együtthatók:

A racionális root-ban kifejezett legalacsonyabb feltételeket., Ez azt jelenti, hogy a P-nek és a q-nak nincsenek közös tényezői. (Ez később fontos lesz.) A számláló osztja az állandót a polinom végén; a demominátor osztja a vezető együtthatót.
példaként:
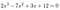
csak a 2.és a 12.,:
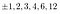
The factors of 2:
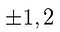
Thus, if a rational root does exist, it’s one of these:
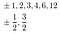
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
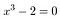
Furthermore:
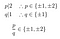
Not one of these candidates qualifies., Ugrás:
A miért
térjünk vissza paradigmapinomunkhoz.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

a Halmozottan mindent qⁿ:

Minden kifejezést a bal oldalon van o közös. Számítsd ki.,

sokkal rosszabbnak tűnik, mint amilyennek lennie kell. A zárójelben lévő összes cuccot helyettesítsük egy s – vel, nem igazán érdekel, mi van benne.
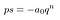
div >
ez sokkal könnyebb a szemen.
ne feledje, hogy P és q egész számok. Nincsenek közös tényezők is., Ezért P nem oszthatja meg a qⁿ-t. A₀:
így a számláló osztja az állandó kifejezést.
most térjen vissza paradigmapinomunkhoz:
ezúttal a rossz az első kifejezés a jobb oldalon.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
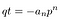
Again, q and p have no common factors. Therefore:
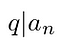
Thus proves the rational root theorem.