a hidrogénatom 1913-as Bohr modelljét 1926-ban a Schrodingerʹs hullámmechanikai modell váltotta fel. A Bohrʹs modellt azonban még ma is nyereségesen tanítják fogalmi és matematikai egyszerűsége miatt, és mivel számos kulcsfontosságú kvantummechanikai ötletet vezetett be, mint például a kvantumszám, a megfigyelhető tulajdonságok kvantálása, a kvantumugrás és a helyhez kötött állapot.,
Bohr számított, hogy a szívócső a szabad elektron energiák által egyensúlyozási a mechanikus erők (centripetális elektron‐mag) egy elektron-végrehajtó kör alakú pályára R sugarú arról, hogy a mag, majd arbitarily kvantálásával az impulzusmomentum. Végül a fiat kijelentette, hogy az elektron nem sugárzó álló állapotban van, mert egy keringő (gyorsító) töltés energiát sugároz, és összeomlik az ellentétes töltésű magba.,
1924‐ben de Broglie posztulált hullám-részecske kettősség az elektron és más hatalmas részecskék számára, ezáltal lehetőséget adva arra, hogy eltávolítsák az arbitritás egy részét a Bohrʹs modellből. Például egy hullám tulajdonságokkal rendelkező elektron konstruktív és destruktív interferenciának van kitéve. Mint látható, ez természetesen az elektron lendület és a kinetikus energia kvantálásához vezet, következésképpen az elektron számára a maghoz viszonyított megengedett energiaállapotok sokaságához., Az itt bemutatott hidrogénatom de Broglie-Bohr modellje az elektronot részecskeként kezeli egy hullámszerű tulajdonságokkal rendelkező gyűrűn.
\
de Broglie hipotézise szerint az anyagnak hullámszerű tulajdonságai vannak.
\
a De Broglieʹs hipotézis következménye; a hullámhossz szerves számának a pálya kerületén belül kell lennie. Ez bevezeti a kvantumszám, amely lehet értékek 1,2,3,… Az N = 4 elektronállapot az alábbiakban látható.,
\
Az első egyenlet helyettesítése a második egyenletbe azt mutatja, hogy a lendület kvantált.
\
Ha a lendület kvantált, akkor a kinetikus energia is.
\
ami azt jelenti, hogy a teljes energia kvantált. A második kifejezés az elektron-proton elektrosztatikus potenciál energiája.
ezeknek a ʺBohr pályáknak a kvantummechanikai értelmezéseʺ az, hogy helyhez kötött állapotok. Annak ellenére, hogy a kinetikus energia kifejezést használjuk, ami elektronmozgást jelent, nincs mozgás., Az elektron részecske-hullámként foglalja el a pályát, nem kering a mag körül. Ha klasszikus értelemben kering, energiát sugároz, és gyorsan összeomlik a magba. Nyilvánvaló, hogy az anyag stabilitása megköveteli a kinetikus energia kvantummechanikai változatát.
a hidrogénatomban lévő elektron földi állapotú energiáját és pályasugarát úgy találjuk meg, hogy az energiát az orbitális sugár függvényében ábrázoljuk. A talajállapot a teljes energiagörbe minimális értéke., Természetesen kalkulus lehet használni, hogy ugyanazt az információt azáltal, hogy minimalizálja az energia tekintetében a pályára sugara. A grafikus módszer azonban az atomstabilitás kérdésének megvilágítása.
alapvető állandók: elektron töltés, elektron tömeg, Planck állandó, vákuum permitivitás.
Quantum number and conversion fact between meters and picometers and joules and attojoules.
\
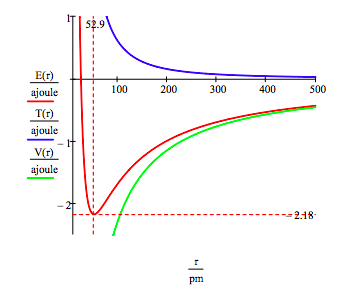
Ez a szám azt mutatja, hogy az atomstabilitás magában foglalja a potenciális és kinetikus energia közötti egyensúlyt., Az elektront a vonzó potenciális energia kölcsönhatás (~ -1/R) vonzza a mag felé, de megakadályozza, hogy a kis pályákhoz kapcsolódó rendkívül nagy kinetikus energia (~1/R2) összeomlik a magba.
az alábbiak szerint a grafikus megközelítés az elektronikus gerjesztett állapotok megtalálására is használható.
\
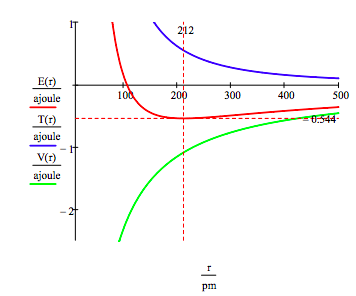
mint korábban említettük, a megengedett elektronenergiák sokrétűsége úgy is előállítható, hogy minimalizálja az energiát az orbitális sugárhoz képest. Ez az eljárás