Trouver les fonctions quadratiques pour les paraboles – Fonctions Quadratiques

Trouver les Fonctions Quadratiques pour les Paraboles

Il ya tellement de différents types de problèmes, vous pouvez être demandé en ce qui concerne des équations quadratiques. Dans cet article, l’accent sera mis sur la façon dont nous pouvons développer une équation quadratique à partir d’un graphe quadratique en utilisant deux méthodes différentes., Mais, avant d’entrer dans ces types de problèmes, prenez un moment pour jouer avec les expressions quadratiques sur cette merveilleuse calculatrice graphique en ligne ici. Plus vous êtes à l’aise avec les graphiques quadratiques et les expressions, plus ce sujet sera facile!

maintenant, commençons à résoudre les problèmes avec cette connaissance, à savoir, comment trouver l’équation d’une parabole!

Comment trouver une équation quadratique à partir d’un graphique:

pour trouver une équation quadratique à partir d’un graphique, il existe deux méthodes simples que l’on peut utiliser: en utilisant 2 points, ou en utilisant 3 points.,

1) Trouver une équation quadratique à partir de 2 Points

pour trouver une équation quadratique à partir d’un graphe utilisant seulement 2 points, l’un de ces points doit être le Sommet. Avec le sommet et un autre point, nous pouvons sous ces coordonnées dans ce qu’on appelle la « forme de sommet » et ensuite résoudre pour notre équation., Le sommet formule suivante, où (d,f) est le sommet le point et (x,y) est l’autre point:

(y±d)=a(x±f)2(y \h d) = a(x \h f)^{2}(y±d)=a(x±f)2

Vertex formulaire peut également être écrit dans sa « bonne » forme », comme:

y=a(x±f)2∓dy = a(x \h f)^{2} \mp dy=a(x±f)2∓d

en Utilisant cette formule, tout ce que nous devons faire est de sub dans le vertex et l’autre point, à résoudre pour un, et alors réécrire l’équation finale., La meilleure façon de devenir à l’aise avec l’utilisation de ce formulaire est de faire un exemple de problème avec elle.

Exemple:

Déterminer l’équation de la parabole indiqué dans l’image ci-dessous.

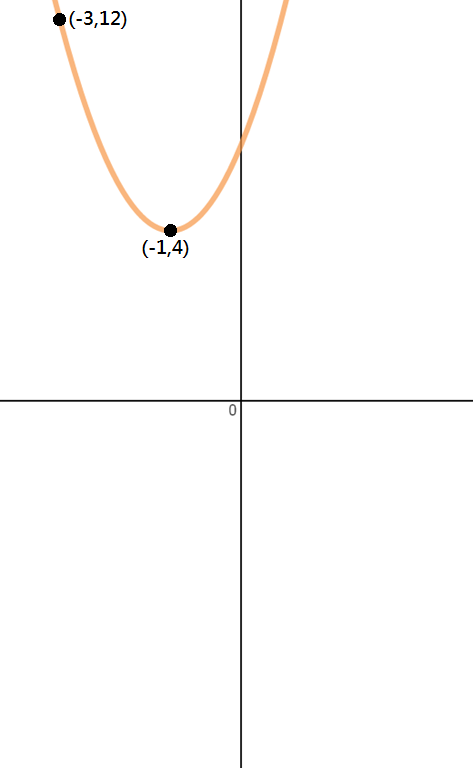
Etape 1: Identifier les Points

Puisque nous sommes à seulement deux points dans ce problème, le sommet et un autre point, nous devons utiliser la forme vertex pour résoudre cette question.,

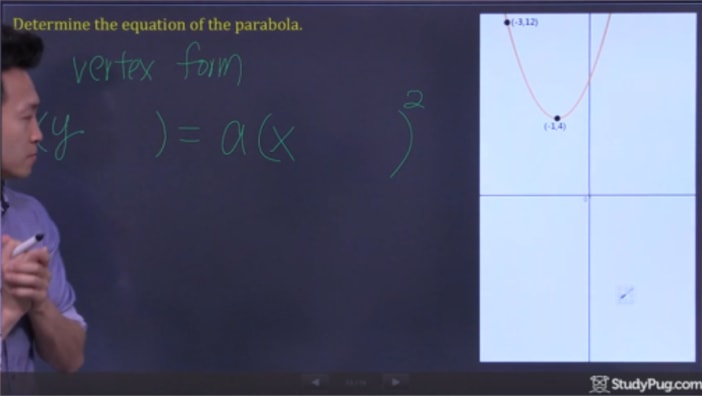
Étape 2: Sous-Points dans la forme de sommet et résoudre pour « a »

maintenant, tout ce que nous avons à faire est de sous dans nos deux points dans la formule des sommets et de résoudre pour « a » d’avoir toutes les informations pour écrire notre équation quadratique finale.,4)=a(-3+1)2(12 – 4) = un(-3 + 1)^{2}(12-4)=un(-3+1)2

8=a(-2)28 = a(-2)^{2}8=a(-2)28=4a8 = 4a8=4aa=2a = 2a=2

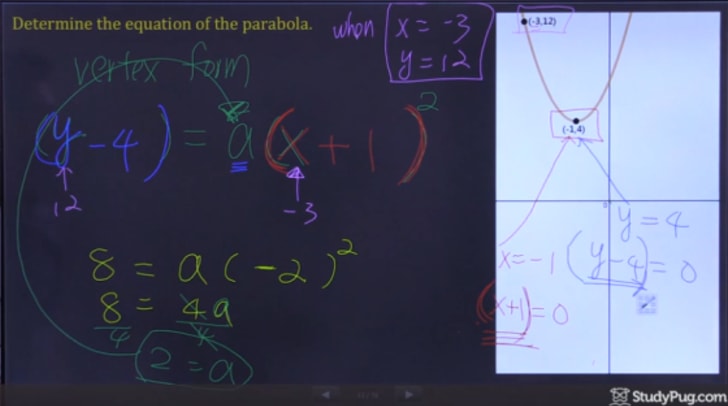
Étape 3: Écrire Équation Quadratique

Après la résolution du « a », nous avons maintenant toutes les informations dont nous avons besoin pour écrire notre réponse finale.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

Et puis, en bon vertex forme d’une parabole, notre réponse finale est:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

Que se termine la leçon sur le vertex de la forme et de la façon de trouver une équation quadratique à partir de 2 points!, Si vous souhaitez vous rafraîchir la mémoire sur des sujets connexes tels que, comment résoudre des expressions quadratiques sous forme de sommet, Comment convertir une équation quadratique régulière de la forme standard en forme de sommet en remplissant le carré, et comment utiliser la formule de sommet, assurez-vous de consulter nos leçons.

2) Trouver L’équation quadratique à partir de 3 Points

Dans certains cas, nous n’aurons pas la chance de recevoir le point sur le Sommet. Si c’est le cas, nous ne pouvons plus trouver l’expression quadratique en utilisant seulement deux points, et nous devons faire quelque chose d’un peu différent., Dans le cas où nous recevons des informations sur les interceptions x d’une parabole, ainsi qu’un autre point, nous pouvons trouver l’équation quadratique en utilisant une équation appelée « forme factorisée ». L’équation générale pour la forme factorisée formule suivante, avec b et c étant l’abscisse les valeurs de la x-intercepte:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

en Utilisant cette formule, tout ce que nous devons faire est de sous dans les coordonnées x des x-intercepte, un autre point, puis de les résoudre pour un si nous pouvons écrire notre réponse finale., Encore une fois, la meilleure façon de devenir à l’aise avec cette forme d’équations quadratiques est de faire un exemple.

Exemple:

Déterminer l’équation de la parabole indiqué dans l’image ci-dessous:

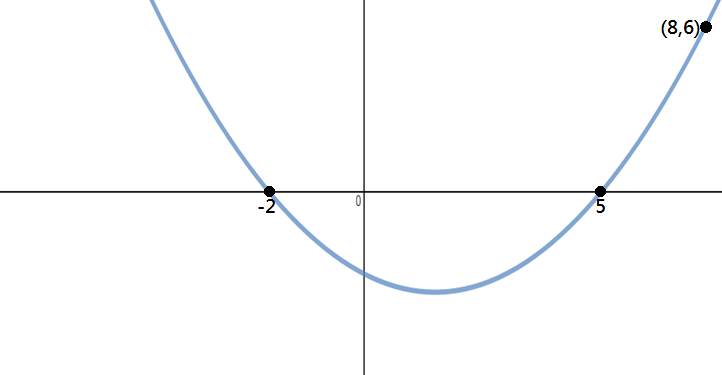
Etape 1: Identifier les Points

Puisque nous sommes donné trois points dans ce problème, le x-intercepte et un autre point, on peut utiliser une forme factorisée de résoudre cette question.,

à partir du graphique, nous pouvons voir que les interceptions x sont -2 et 5, et le point sur la parabole est (8,6).

Étape 2: sous-Points sous forme de sommet et résoudre pour « a »

maintenant, tout ce que nous avons à faire est de sous-dans nos valeurs dans la formule de forme factorisée et de résoudre pour « a » pour avoir toutes les informations pour écrire notre équation quadratique finale.,(x – 5)y=(x+2)(x−5)

Ensuite, on peut utiliser le point sur la parabole (8,6) à résoudre pour la « une »:

6=un(8+2)(8-5)6 = un(8 + 2)(8 – 5)6=un(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30aa=15a = \frac{1}{5}a=51

l’Étape 3: Écrire Équation Quadratique

Après la résolution du « a », nous avons maintenant toutes les informations dont nous avons besoin pour écrire notre réponse finale.,

y=15(x+2)(x−5)y = \frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

Et c’est tout là est à lui! Ce sont les deux méthodes les plus importantes pour trouver une fonction quadratique à partir d’une parabole donnée. Pour une étude plus approfondie des fonctions quadratiques et de leurs graphiques, consultez ces vidéos utiles traitant du discriminant, des inégalités quadratiques et des sections coniques.