Moment D’inertie, forme générale
étant donné que le moment d’inertie d’un objet ordinaire implique une distribution continue de la masse à une distance variant continuellement de tout axe de rotation, le calcul des moments d’inertie implique généralement le calcul, La discipline des mathématiques qui, Puisque le moment d’inertie d’une masse ponctuelle est défini par
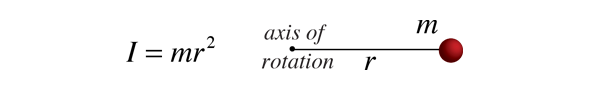
alors le moment d’inertie contribution par un élément de masse infinitésimale DM a la même forme. Ce type de masse d’élément est appelé un élément différentiel de masse et son moment d’inertie est donnée par

Notez que la différentielle de l’élément de moment d’inertie dI doit toujours être définie par rapport à un axe de rotation., La somme sur tous ces éléments de masse est appelée intégrale sur la masse.
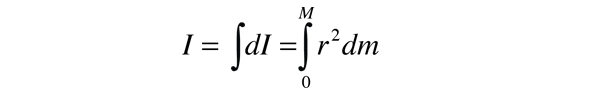
Habituellement, la masse de l’élément dm seront exprimés en termes de la géométrie de l’objet, de sorte que l’intégration peut être effectuée sur l’objet comme un tout (par exemple, sur une longue uniforme de la tige).
ayant appelé cela une forme générale, il est probablement approprié de souligner que c’est une forme générale uniquement pour les axes qui peuvent être appelés « axes principaux », un terme qui inclut tous les axes de symétrie des objets., Le concept de moment d’inertie pour les objets généraux sur les axes arbitraires est un sujet beaucoup plus compliqué. Le moment d’inertie dans de tels cas prend la forme d’une grandeur tensorielle mathématique qui nécessite neuf composantes pour la définir complètement.
| Exemples d’intégration pour obtenir le moment d’inertie. | tige Droite |
| Cylindre | |
| Sphère |