Le théorème de Bayes trouve de nombreuses utilisations dans la théorie des probabilités et les statistiques. Il y a une micro chance que vous n’ayez jamais entendu parler de ce théorème dans votre vie. Il s’avère que ce théorème a trouvé son chemin dans le monde de l’apprentissage automatique, pour former l’un des algorithmes très décorés. Dans cet article, nous allons tout apprendre sur L’algorithme naïf de Bayes, ainsi que ses variations à des fins différentes dans l’apprentissage automatique.
comme vous l’avez peut-être deviné, cela nous oblige à voir les choses d’un point de vue probabiliste., Tout comme dans l’apprentissage automatique, nous avons des attributs, des variables de réponse et des prédictions ou des classifications. En utilisant cet algorithme, nous allons traiter les distributions de probabilité des variables dans l’ensemble de données et prédire la probabilité de la variable de réponse appartenant à une valeur particulière, compte tenu des attributs d’une nouvelle instance. Commençons par revoir le théorème de Bayes.
théorème de Bayes
ceci nous permet d’examiner la probabilité d’un événement basé sur la connaissance préalable de tout événement lié au premier événement., Ainsi, par exemple, la probabilité que le prix d’une maison est élevé, peut être mieux évaluée si nous connaissons les installations autour d’elle, par rapport à l’évaluation faite sans la connaissance de l’emplacement de la maison. Le théorème de Bayes fait exactement cela.

Équation ci-dessus donne la représentation de base du théorème de Bayes., Ici A et B sont deux événements et,
P(A / B) : la probabilité conditionnelle que L’événement A se produise , étant donné que B s’est produit. Ceci est également connu comme la probabilité postérieure.
P(A) et P (B) : Probabilité de A et B sans égard l’un de l’autre.
P(B / A) : la probabilité conditionnelle que L’événement B se produise , étant donné que A s’est produit.
maintenant, voyons comment cela convient bien au but de l’apprentissage automatique.,
prenons un simple problème d’apprentissage automatique, où nous devons apprendre notre modèle à partir d’un ensemble donné d’attributs(dans des exemples de formation), puis former une hypothèse ou une relation avec une variable de réponse. Ensuite, nous utilisons cette relation pour prédire une réponse, en fonction des attributs d’une nouvelle instance. En utilisant le théorème de Bayes, il est possible de construire un apprenant qui prédit la probabilité de la variable de réponse appartenant à une classe, compte tenu d’un nouvel ensemble d’attributs.
examinez à nouveau l’équation précédente. Maintenant, supposons que A est la variable de réponse et B est l’attribut d’entrée., Donc, selon l’équation, nous avons
P(A|B) : probabilité conditionnelle de variable de réponse appartenant à une valeur particulière, compte tenu des attributs d’entrée. Ceci est également connu comme la probabilité postérieure.
P(A) : la probabilité antérieure de la variable de réponse.
P(B) : la probabilité de données d’entraînement ou les preuves.
P(B|A) : c’est ce qu’on appelle la probabilité des données d’entraînement.,
Donc, l’équation ci-dessus peut être réécrite sous la forme
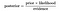
prenons un problème, où le nombre d’attributs est égal à n et la réponse est une valeur booléenne, c’est à dire qu’il peut être dans l’une des deux classes. En outre, les attributs sont catégoriques (2 catégories pour notre cas). Maintenant, pour former le classificateur, nous devrons calculer P (B / A), pour toutes les valeurs de l’instance et de l’espace de réponse., Cela signifie que nous devrons calculer 2*(2^n -1), paramètres pour apprendre ce modèle. C’est clairement irréaliste dans la plupart des domaines d’apprentissage. Par exemple, s’il y a 30 attributs booléens, nous devrons estimer plus de 3 milliards de paramètres.
algorithme de Bayes naïf
la complexité du Classificateur bayésien ci-dessus doit être réduite pour être pratique. L’algorithme naïf de Bayes le fait en faisant une hypothèse d’indépendance conditionnelle sur l’ensemble de données d’entraînement. Cela réduit considérablement la complexité du problème mentionné ci-dessus à seulement 2n.,
L’hypothèse de l’indépendance conditionnelle stipule que, étant donné les variables aléatoires X, Y et Z, nous disons que X est conditionnellement indépendant de Y étant donné Z, si et seulement si la distribution de probabilité régissant X est indépendante de la valeur de Y étant donné Z.
En d’autres termes, X et Y sont conditionnellement indépendants étant donné Z si et seulement si, étant donné la connaissance que Z se produit, la connaissance de savoir si X se produit ne fournit aucune information sur la probabilité que Y se produise, et la connaissance de savoir si Y se produit ne fournit aucune information sur la probabilité que X se produise.,
Cette hypothèse rend l’algorithme de Bayes, naïf.
etant Donné, n différentes valeurs de l’attribut, la probabilité peut maintenant être écrite sous la forme
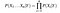
Ici, X représente les attributs ou des caractéristiques, et Y est la variable de réponse. Maintenant, P (X|Y) devient égal aux produits de, distribution de probabilité de chaque attribut X donné Y.,
maximiser a Posteriori
ce qui nous intéresse, c’est de trouver la probabilité postérieure ou P(Y / X). Maintenant, pour plusieurs valeurs de Y, nous devrons calculer cette expression pour chacune d’elles.
étant donné une nouvelle instance Xnew, nous devons calculer la probabilité que Y prenne une valeur donnée, compte tenu des valeurs d’attribut observées de Xnew et des distributions P(Y) et P(X / Y) estimées à partir des données d’apprentissage.
alors, comment allons-nous prédire la classe de la variable de réponse, en fonction des différentes valeurs que nous atteignons pour P(Y / X)., Nous prenons simplement la plus probable ou maximale de ces valeurs. Par conséquent, cette procédure est également connue sous le nom de maximisation a posteriori.
maximum de Vraisemblance
Si nous supposons que la variable de réponse est uniformément distribué, c’est qu’il est tout aussi susceptibles d’obtenir une quelconque réponse, alors nous pouvons simplifier l’algorithme. Avec cette hypothèse, le priori ou P (Y) devient une valeur constante, qui est 1/catégories de la réponse.
comme les priori et les preuves sont maintenant indépendants de la variable de réponse, ceux-ci peuvent être retirés de l’équation., Par conséquent, la maximisation a posteriori est réduite à la maximisation du problème de probabilité.
distribution des entités
Comme vu ci-dessus, nous devons estimer la distribution de la variable de réponse à partir de l’ensemble d’apprentissage ou supposer une distribution uniforme. De même, pour estimer les paramètres de la distribution d’une entité, il faut supposer une distribution ou générer des modèles non paramétriques pour les entités à partir de l’ensemble d’apprentissage. De telles hypothèses sont connues sous le nom de modèles d’événements. Les variations de ces hypothèses génèrent différents algorithmes à des fins différentes., Pour les distributions continues, le Bayes naïf gaussien est l’algorithme de choix. Pour les entités discrètes, les distributions multinomiales et Bernoulli sont populaires. Une discussion détaillée de ces variations est hors du champ d’application de cet article.
les classificateurs naïfs Bayes fonctionnent très bien dans des situations complexes, malgré les hypothèses simplifiées et la naïveté. L’avantage de ces classificateurs est qu’ils nécessitent un petit nombre de données d’apprentissage pour estimer les paramètres nécessaires pour la classification. C’est l’algorithme de choix pour la catégorisation de texte., C’est l’idée de base derrière les classificateurs naïfs Bayes, que vous devez commencer à expérimenter avec l’algorithme.