
Une brève explication et la preuve
La Racine Rationnelle Théorème (TRA) est un outil pratique à avoir dans votre arsenal mathématique. Il fournit et test rapide et sale pour la rationalité de certaines expressions. Et cela aide à trouver les racines rationnelles des polynômes.,
Voici comment et pourquoi il fonctionne.,e53714″>
Comment
Supposons que vous avez un polynôme de degré n, à coefficients entiers:

La Racine Rationnelle Théorème dit: Si une racine rationnelle existe, puis ses composants seront diviser le premier et le dernier coefficients:

Le rationnel de la racine est exprimé en termes plus bas., Cela signifie que p et q ne partagent aucun facteur commun. (Ce sera important plus tard.) Le numérateur divise la constante à la fin du polynôme; le démominateur divise le coefficient principal.
un exemple:
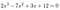
il Nous suffit de regarder le 2 et le 12.,:
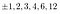
The factors of 2:
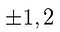
Thus, if a rational root does exist, it’s one of these:
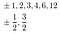
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
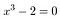
Furthermore:
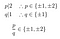
Not one of these candidates qualifies., Vous pouvez également utiliser la fonction div id= »4481b26f11″>
le pourquoi
revenons à notre paradigme Polynomial.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Multipliez le tout par qⁿ:

Chaque terme, la gauche a p en commun. Facteur de cela.,

Il est bien pire que ce qu’elle doit être. Remplaçons tout cela entre parenthèses par un s. Nous ne nous soucions pas vraiment de ce qu’il y a dedans.
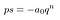
C’est beaucoup plus facile sur les yeux.
rappelez-vous que p et q Sont des entiers. Ils ne partagent pas non plus de facteurs communs., Par conséquent, p ne peut pas diviser qⁿ. Il faut diviser a₀:
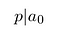
Ainsi, le numérateur divise le terme constant.
Maintenant, retournez à notre paradigme polynôme:

Cette fois, le mauvais, le premier terme du côté droit.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
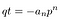
Again, q and p have no common factors. Therefore:
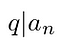
Thus proves the rational root theorem.