formes tridimensionnelles: Polyèdres, solides courbes et surface

Cette page examine les propriétés des formes tridimensionnelles ou « solides ».

une forme bidimensionnelle a une longueur et une largeur. Une forme solide tridimensionnelle a également de la profondeur. Les formes tridimensionnelles, de par leur nature, ont un intérieur et un extérieur, séparés par une surface. Tous les objets physiques, les choses que vous pouvez toucher, sont en trois dimensions.,

cette page couvre à la fois les solides droits appelés polyèdres, qui sont basés sur des polygones, et les solides avec des courbes, tels que des globes, des cylindres et des cônes.

Polyèdres

les polyèdres (ou polyèdres) sont des formes solides droites. Les polyèdres sont basés sur des polygones, des formes planes bidimensionnelles avec des lignes droites.

consultez notre page Propriétés des polygones pour en savoir plus sur l’utilisation des polygones.

les polyèdres sont définis comme ayant:

• bords droits.
• côtés plats appelés faces.,
• coins, appelés sommets.

les polyèdres sont également souvent définis par le nombre d’arêtes, de faces et de Sommets qu’ils ont, ainsi que par le fait que leurs faces aient toutes la même forme et la même taille. Comme les polygones, les polyèdres peuvent être réguliers (basés sur des polygones réguliers) ou irréguliers (basés sur des polygones irréguliers). Les polyèdres peuvent également être concaves ou convexes.

l’un des polyèdres les plus basiques et familiers est le cube. Un cube est un polyèdre régulier, ayant six faces carrées, 12 arêtes et huit sommets.,

Polyèdres Réguliers (Platonique Solides)

Les cinq solides réguliers sont une classe spéciale de polyèdres, dont toutes les faces sont identiques, chaque face étant un polygone régulier. Les solides platoniques sont:

• tétraèdre à quatre faces triangulaires équilatérales.
• Cube à six faces carrées.
• octaèdre avec huit faces triangulaires équilatérales.
• Dodécaèdre à douze faces pentagonales.
• icosaèdre avec vingt faces triangulaires équilatérales.,

Voir le schéma ci-dessus pour une illustration de chacun de ces polyèdres réguliers.

qu’est Ce qu’un Prisme?

un prisme est un polyèdre qui a deux extrémités et des côtés plats correspondants. Si vous coupez un prisme n’importe où sur sa longueur, parallèlement à une extrémité, sa section est la même-vous vous retrouverez avec deux prismes. Les côtés d’un prisme sont des parallélogrammes – des formes à quatre côtés avec deux paires de côtés de longueur égale.

Les Antiprismes sont similaires aux prismes réguliers, leurs extrémités correspondent., Cependant, les côtés des anti-prismes sont constitués de triangles et non de parallélogrammes. Les antiprismes peuvent devenir très complexes.

qu’est Ce qu’une Pyramide?

une pyramide est un polyèdre avec une base polygonale qui se connecte à un sommet (point supérieur) avec des côtés droits.

bien que nous ayons tendance à penser à des pyramides à base carrée, comme celles construites par les anciens Égyptiens, elles peuvent en fait avoir n’importe quelle base polygonale, régulière ou irrégulière. De plus, une pyramide peut avoir un sommet au centre direct de sa base, une pyramide droite, ou peut avoir l’apex excentré lorsqu’il s’agit d’une pyramide Oblique.,

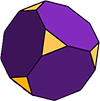
Polyèdres plus complexes

Il existe de nombreux autres types de polyèdres: symétriques et asymétriques, concaves et convexes.

Levier solides, par exemple, sont constitués d’au moins deux polygones réguliers.

Le cube tronqué (comme illustré) est un solide D’Archimède à 14 faces. 6 des faces sont des octogones réguliers et les 8 autres sont des triangles réguliers (équilatéraux). La forme a 36 arêtes et 24 sommets (coins).,

les formes tridimensionnelles avec des courbes

Les formes solides qui comprennent un bord incurvé ou rond ne sont pas des polyèdres. Les polyèdres ne peuvent avoir que des côtés droits.

de Nombreux objets autour de vous inclure au moins quelques courbes. En Géométrie, les solides courbes les plus courants sont les cylindres, les cônes, les sphères et les tores (le pluriel pour tore).,

Commune des Formes en Trois Dimensions avec des Courbes:
Cylindre	Cône
Une bouteille a la même section d’un bout à l’autre. Les cylindres ont deux extrémités identiques d’un cercle ou d’un ovale. Bien que similaires, les cylindres ne sont pas des prismes car un prisme a (par définition) un parallélogramme, des côtés plats.,	un cône a une base circulaire ou ovale et un sommet (ou Sommet). Le côté du cône se rétrécit doucement jusqu’à l’apex. Un cône est similaire à une pyramide mais distinct comme un cône a un seul côté incurvé et une base circulaire.
Sphère	Torus
la Forme d’une balle ou d’un globe, une sphère est complètement un objet rond. Chaque point sur la surface d’une sphère est égale distance du centre de la sphère.,	en forme d’anneau, de pneu ou de beignet, un tore annulaire régulier est formé en tournant un cercle plus petit autour d’un cercle plus grand. Il existe également une forme plus complexe de tores.

Surface

notre page sur le calcul de la surface explique comment calculer la surface des formes bidimensionnelles et vous devez comprendre ces bases afin de calculer la surface des formes tridimensionnelles.

pour les formes tridimensionnelles, on parle de surface, pour éviter toute confusion.,

Vous pouvez utiliser vos connaissances sur l’aire des formes bidimensionnelles pour calculer la surface d’une forme tridimensionnelle, car chaque face ou côté est effectivement une forme bidimensionnelle.

Vous déterminez donc la zone de chaque face, puis vous les additionnez.

Comme avec les formes plates, la surface d’un solide est exprimée en unités carrées: cm2, inches2, m2 et ainsi de suite. Vous trouverez plus de détails sur les unités de mesure sur notre page systèmes de mesure.,

exemples de calculs de Surface

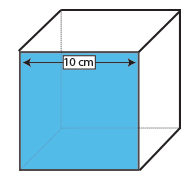
Cube

La surface d’un cube est l’aire d’une face (longueur x Largeur) multipliée par 6, car les six faces sont identiques.

comme la face d’un cube est un carré, il suffit de prendre une mesure – la longueur et la largeur d’un carré sont, par définition, les mêmes.

Une face de ce cube vaut donc 10 × 10 cm = 100cm2. Multiplier par 6 le nombre de faces d’un cube, et nous constatons que la surface de ce cube est 600cm2.,

autres polyèdres réguliers

de même, la surface des autres polyèdres réguliers (solides platoniques) peut être calculée en trouvant l’aire d’un côté, puis en multipliant la réponse par le nombre total de côtés – voir le diagramme de polyèdres de base ci-dessus.

Si l’aire d’un pentagone constituant un dodécaèdre est de 22cm2 alors multipliez ceci par le nombre total de côtés (12) pour donner la réponse 264cm2.,

pyramide

pour calculer la surface d’une pyramide standard avec quatre côtés triangulaires égaux et une base carrée:

commencez par déterminer la surface de la base (carrée) longueur × largeur.

ensuite, déterminez l’aire d’un côté (triangle). Mesurez la largeur le long de la base, puis la hauteur du triangle (également connu sous le nom de longueur inclinée) du point central de la base au sommet.,

Vous pouvez alors soit diviser votre réponse par 2 pour vous donner la surface d’un triangle, puis multiplier par 4 pour donner la surface des quatre côtés, soit simplement multiplier la surface d’un triangle par 2.

enfin, additionnez la surface de la base et des côtés pour trouver la surface totale de la pyramide.

pour calculer la surface d’autres types de pyramide, additionnez la surface de la base (connue sous le nom de surface de base) et la surface des côtés (surface latérale), vous devrez peut-être mesurer les côtés individuellement.,

diagrammes de réseau

un réseau géométrique est un « motif » bidimensionnel pour un objet tridimensionnel. Les filets peuvent être utiles lors de l’élaboration de la surface d’un objet tridimensionnel. Dans le diagramme ci-dessous, vous pouvez voir comment les pyramides de base sont construites, si la pyramide est « dépliée », vous vous retrouvez avec le filet.

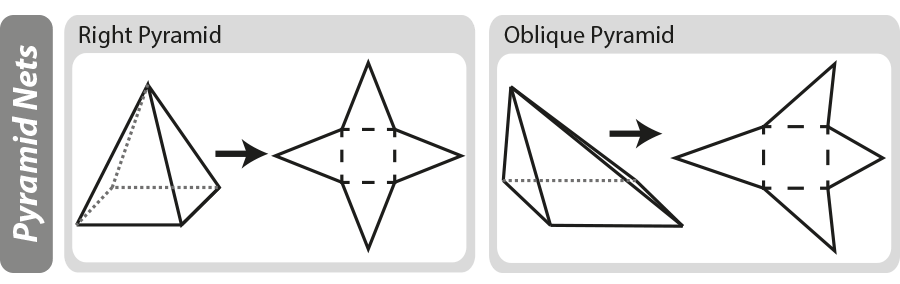
pour plus d’informations sur les diagrammes de réseau, consultez notre page formes et réseaux 3D.

Prism

Pour calculer la surface d’un prisme:

Prismes ont deux extrémités de la même et plat côtés du parallélogramme.,

calculez l’aire d’une extrémité et multipliez par 2.

pour un prisme régulier (où tous les côtés sont identiques), calculez l’aire de l’un des côtés et multipliez par le nombre total de côtés.

pour les prismes irréguliers (avec des côtés différents) calculer l’aire de chaque côté.

Ajoutez vos deux réponses ensemble (extrémités × côtés) pour trouver la surface totale du prisme.,

Cylindre

Pour calculer la surface d’un cylindre, il est utile de réfléchir sur les composantes de la forme. Imaginez une boîte de maïs doux – elle a un haut et un bas, qui sont tous deux cercles. Si vous coupez le côté le long de sa longueur et que vous l’aplatissez, vous aurez un rectangle. Vous devez donc trouver l’aire de deux cercles et un rectangle.

commencez par déterminer l’aire d’un des cercles.

L’aire d’un cercle est π(pi) × radius2.,

en Supposant un rayon de 5 cm, l’aire de l’un des cercles est de 3,14 × 52 = 78.5cm2.

Multiplier la réponse par 2, comme il y a deux cercles 157cm2

La zone du côté du cylindre est le périmètre du cercle × la hauteur du cylindre.

le périmètre est égal à π x 2 × rayon. Dans notre exemple, 3.14 × 2 × 5 = 31.4

Mesurer la hauteur du cylindre – pour cet exemple, la hauteur est de 10 cm. La surface du côté est de 31,4 × 10 = 314cm2.,

La surface totale peut être trouvé par l’ajout de la zone de cercles et de la côte:

157 + 314 = 471cm2

Cône

Lorsque le calcul de la surface d’un cône, vous devez utiliser la longueur de la « slant » ainsi que le rayon de la base.

Cependant, il est relativement simple à calculer:

L’aire du cercle à la base du cône est, π(pi) × radius2.

Dans cet exemple, la somme est 3.14 × 52 = 3.14 × 25 = 78.,5cm2

la surface du côté, la section inclinée, peut être trouvée en utilisant cette formule:

π(pi) × rayon × longueur de l’inclinaison.

Dans notre exemple, la somme est de 3,14 × 5 × 10 = 157cm2.

enfin, ajoutez la zone de base à la zone latérale pour obtenir la surface totale du cône.

78.5 + 157 = 235.5cm2

Sphère

La surface d’une sphère est relativement simple extension de la formule pour un cercle de la région.

4 × π × radius2.,

pour une sphère, il est souvent plus facile de mesurer le diamètre – la distance à travers la sphère. Vous pouvez alors trouver le rayon qui est la moitié du diamètre.

Le diamètre d’une balle de tennis standard est de 2,6 pouces. Le rayon est donc de 1,3 pouces. Pour la formule, nous avons besoin du rayon au carré. 1.3 × 1.3 = 1.69.

la surface d’une balle de tennis est donc:

4 × 3,14 × 1,69 = 21,2264 pouces2.,

Torus

pour calculer la surface d’un tore, vous devez trouver deux valeurs de rayon.

Le grand ou le grand rayon (R) est mesuré du milieu du trou au milieu de l’anneau.

le petit ou le petit rayon (r) est mesuré du milieu de l’anneau au bord extérieur.

le diagramme montre deux vues d’un exemple de tore et comment mesurer ses rayons (ou rayons).,

le calcul de La surface est en deux parties (une pour chaque rayon). Le calcul est le même pour chaque partie.

la formule est: surface area = (2NR)(2nr)

pour calculer la surface du tore exemple.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

Multipliez les deux réponses pour trouver la surface totale de l’exemple du tore.