Calculate Log & Antilog Online (Français)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

Où

• b = base,
• y = nombre,
• x = valeur du journal.

le Calcul de Antilog:

y = 10x

Où

• x = le nombre,
• y = antilog valeur.

logarithmes et anti-logarithmes: comment cela fonctionne et son importance

– Guide rédigé par Corin B. Arenas, publié le 1er octobre 2019

Si vous vous êtes déjà demandé comment les experts déterminent les grandes distances, l’intensité des tremblements de terre et les taux de croissance économique mondiale, alors vous êtes au bon endroit.

calculer des sommes très importantes peut être lent et déroutant., Mais avec l’aide de logarithmes (log) et d’antilogarithmes (antilog), les calculs peuvent être simplifiés.

lisez la suite pour en savoir plus sur log et antilog, comment ils fonctionnent et pourquoi il s’agit de concepts mathématiques pertinents.

Qu’est-ce que le logarithme?

Un logarithme est la puissance d’un nombre (appelée base) doit être multiplié à lui-même pour obtenir un nombre donné. En termes plus simples, le logarithme résout le problème:

combien de fois multiplions-Nous b pour obtenir un autre nombre y?,

Logarithme compte le nombre de fois que le même facteur doit être multipliée pour arriver à un nombre donné.

Qui est Venu avec Elle?

Log a été inventé au 16ème siècle comme outil de calcul par le mathématicien, physicien et astronome écossais John Napier. Il a écrit le livre Mirifici Logarithmorum Canonis Descriptio avec des tables et des nombres discutant des logarithmes naturels, jetant les bases de son concept de base.

Napier a inventé le terme logarithme du mot grec logos qui signifie « rapport ou proportion », et arithmos qui signifie « nombre »., »Lorsqu’il est combiné, cela signifie littéralement » nombre de rapport.’

2 types de logarithmes

le logarithme naturel d’un nombre est son logarithme à la base de la constante e, où e est approximativement égal à 2,718281828459. L’équation s’écrit loge(x).

Si un logarithme ne spécifie pas de base, comme cet exemple: log(1000), il est connu comme un logarithme commun qui utilise la base 10.

log(1000), il est connu comme un logarithme commun qui utilise la base 10.

comment le Log est-il utilisé?,

Une fois que vous commencez à calculer des chiffres par millions, milliards et trillions, cela peut devenir assez taxant. Qu’il s’agisse de compter beaucoup d’argent, de la croissance des populations ou de couvrir de grandes distances, log peut fonctionner pour vous. Il peut simplifier les grandes sommes qui impliquent des équations longues et déroutantes, les rendant plus faciles à saisir.

Voici l’équation standard pour connecter:
logb(x) = y

Où

• Le nombre multiplié à lui-même (b) est la base.
• Le nombre de fois qu’il est multiplié (y) est le logarithme.,
• Le nombre obtenu (x) est écrit entre parenthèses.

pour comprendre comment fonctionne le concept, voici un exemple avec un nombre plus petit:
Question: Combien de 2s multiplions-nous pour obtenir 32?
b = 2, x = 32

log2(32) = y
Réponse: 2 x 2 x 2 x 2 x 2 = 32

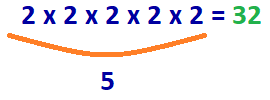
5 numéro 2 doit être multipliée pour obtenir le numéro 32.
La réponse: log2(32) = 5

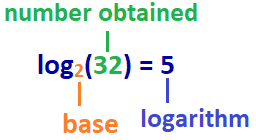
Donc, dans cet exemple: le logarithme de La 32 à la base 2 est 5, ou logarithme de base 2 de 32 est 5.,

de plus, log est la fonction inverse de l’exponentiation, où l’opération mathématique s’écrit bn. b est la base qui est multipliée par la puissance de n, Qui est le nombre de fois qu’elle est multipliée par elle-même.

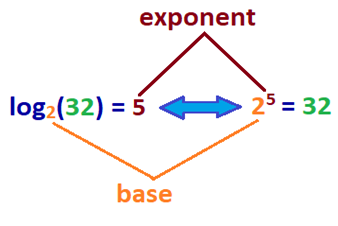
Qu’est-ce que cela signifie? Le log d’un nombre est l’exposant auquel la base b est multipliée pour obtenir un nombre donné. Pour vous donner une meilleure idée, reportez-vous à l’exemple d’équation log définie à côté de son équation exponentielle ci-dessous.,

log	exposant
log2(32) = 5	25 = 32

Maintenant, nous allons essayer avec un grand nombre.
Question: Combien de 10s multiplions-nous pour obtenir 150 000 000 000?
b = 10, x = 150,000,000,000

logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.,1760912590557

ceci est résolu en utilisant la fonction log dans une calculatrice scientifique. Ou utiliser la calculatrice sur cette page pour obtenir la réponse.

comment L’antilogarithme est-il lié au Log?

Un numéro de journal peut alors être retourné à son numéro d’origine. Cela peut être fait en utilisant antilogarithme (antilog). Ainsi, l’antilog est la fonction inverse de log. De même, antilog fonctionne pour exponentier une valeur de journal simplifiée.,

pour calculer l’antilog d’un nombre y, vous devez élever le logarithme de base b (Généralement 10, parfois la constante e) à la puissance qui générera le nombre Y.

Voici L’équation pour l’antilog en utilisant la base 10:
10x = y
où x est l’exposant et y est la valeur antilog.

Par exemple, si nous prenons cette équation, log(5) = x, son antilog sera 10x = 5.

• Log: (5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

Maintenant, nous allons essayer avec un plus grand nombre.,

Si nous prenons log(150,000,000,000) = x, son antilog sera 10x = 150,000,000,000.

• Log: log10(150,000,000,000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150,000,000,000

Importance et Applications réelles

avant l’invention des calculatrices, les logarithmes étaient utilisés pour simplifier les calculs dans divers domaines de la connaissance, tels que la navigation, l’arpentage, l’astronomie, et plus tard, l’ingénierie.

imaginez naviguer au milieu de nulle part au 16ème siècle., À l’époque, les navigateurs s’appuyaient sur la position des étoiles et un mécanisme de sextant pour déterminer leur emplacement exact. Sans technologie moderne pour vous aider à calculer de grandes distances, vous pouvez utiliser log pour simplifier vos calculs. La précision est importante, ou vous risquez plus de jours en mer avec de maigres Fournitures. Moins d’équations signifient moins de marge d’erreur.

Qu’en est-il des autres applications pratiques? Les logarithmes des États Scientifiques vivants relient les progressions géométriques aux progressions arithmétiques., Si vous avez déjà remarqué des formes et des motifs répétitifs dans la nature, l’architecture et l’art, ces formations possèdent leurs propres valeurs logarithmiques correspondantes.

Aujourd’hui, la connaissance de la façon dont ces modèles fonctionnent influence la façon dont l’humanité construit et conçoit des maisons, des bâtiments et des paysages urbains.

Logarithmes sont également utilisés pour exprimer l’étendue et l’intensité de certaines échelles., Outre les grandes distances et les vitesses élevées, il mesure d’autres choses telles que:

• intensité sonore
• fréquence sonore
• Force des tempêtes de vent
• force des tremblements de terre
• niveau corrosif des acides
• dureté des minéraux
• luminosité des étoiles

prenons l’exemple des décibels. Pour rendre les haut-parleurs plus forts de 10 décibels, ils doivent être alimentés par 10 fois la puissance. Comme vous l’augmentez à + 20 dB, il aura besoin de 100 fois la puissance, et de +30 dB, il aura besoin de 1 000 la puissance.

de plus, l’intensité sonore progresse arithmétiquement., Il change également proportionnellement avec le logarithme d’une onde sonore qui progresse géométriquement.

ci-dessous est un tableau de Live Science énumérant différentes échelles logarithmiques avec leurs échelles linéaires correspondantes.

dans la mesure des taux et des rangs

selon Kalid Azad, l’éducateur en mathématiques derrière BetterExplained.com, les logarithmes sont la façon dont nous comprenons à quelle vitesse quelque chose grandit.

Commune logarithmes fondamentalement décrire en termes de leurs puissances de 10. En ce qui concerne le taux d’intérêt, le logarithme est la croissance d’un investissement.,

pour déterminer le taux de croissance du PIB d’un pays, les analystes examinent le PIB des années suivantes. Ils prennent le PIB de l’année précédente et le PIB de l’année suivante, puis calculent le logarithme pour trouver le taux de croissance estimé.

Les moteurs de recherche utilisent le graphique de liens pour aider à évaluer l’importance, la fiabilité& autorité des documents sur le web. PageRank de Google a été une évolution majeure dans la recherche qui a stimulé la pertinence de la recherche et a aidé Google Recherche marketshare.,

Selon Azad, dans une échelle de 1 à 10, une landing page avec un PageRank de 2 est 10 fois plus populaire qu’une page avec un PageRank de 1. Si un site a un PageRank de 5 et un concurrent site a un PageRank de 9, il a une différence de 4 ordres de grandeur.

un ordre de grandeur signifie à peu près une différence 10x, ou un classement est 1 chiffre plus grand par rapport à l’autre. Dans ce cas, un site avec un PageRank 9 est 100 000 000 plus populaire qu’un site avec un PageRank 1.,

the Bottom Line

Log et antilog sont des méthodes de calcul importantes qui nous permettent de simplifier de grandes sommes. La simplification raccourcit le processus de calcul et facilite la compréhension des calculs. Cela permet de réduire la marge d’erreur.

de plus, l’utilisation de log fournit des échelles mesurables pour mesurer les phénomènes naturels, comme l’intensité des tremblements de terre, la force des tempêtes de vent et la luminosité des étoiles. En termes de finance, les logarithmes nous permettent d’identifier les taux d’intérêt et les taux de croissance économique.

Il est pratiquement utilisé dans de nombreux domaines., Les grandes valeurs qui dépendent de la précision de la mesure bénéficient de l’utilisation de calculs logarithmiques.

à propos de l’auteur

Corin est un ardent chercheur et écrivain de sujets financiers—étudiant les tendances économiques, comment elles affectent les populations, ainsi que comment aider les consommateurs à prendre des décisions financières plus sages. Ses autres articles de fond peuvent être lus Inquirer.net et Manileno.com. elle est titulaire d’une Maîtrise en écriture créative de L’Université des Philippines, l’une des meilleures institutions académiques au monde, et D’une licence en arts de la Communication du Miriam College.