la relation entre la pression et le Volume: loi de Boyle
lorsque la pression sur un gaz augmente, le volume du gaz diminue parce que les particules de gaz sont Inversement, à mesure que la pression sur un gaz diminue, le volume de gaz augmente car les particules de gaz peuvent maintenant s’éloigner., Les ballons météorologiques grossissent à mesure qu’ils s’élèvent dans l’atmosphère vers des régions de pression plus basse car le volume du gaz a augmenté; c’est-à-dire que le gaz atmosphérique exerce moins de pression à la surface du ballon, de sorte que le gaz intérieur se dilate jusqu’à ce que les pressions internes et externes soient égales.
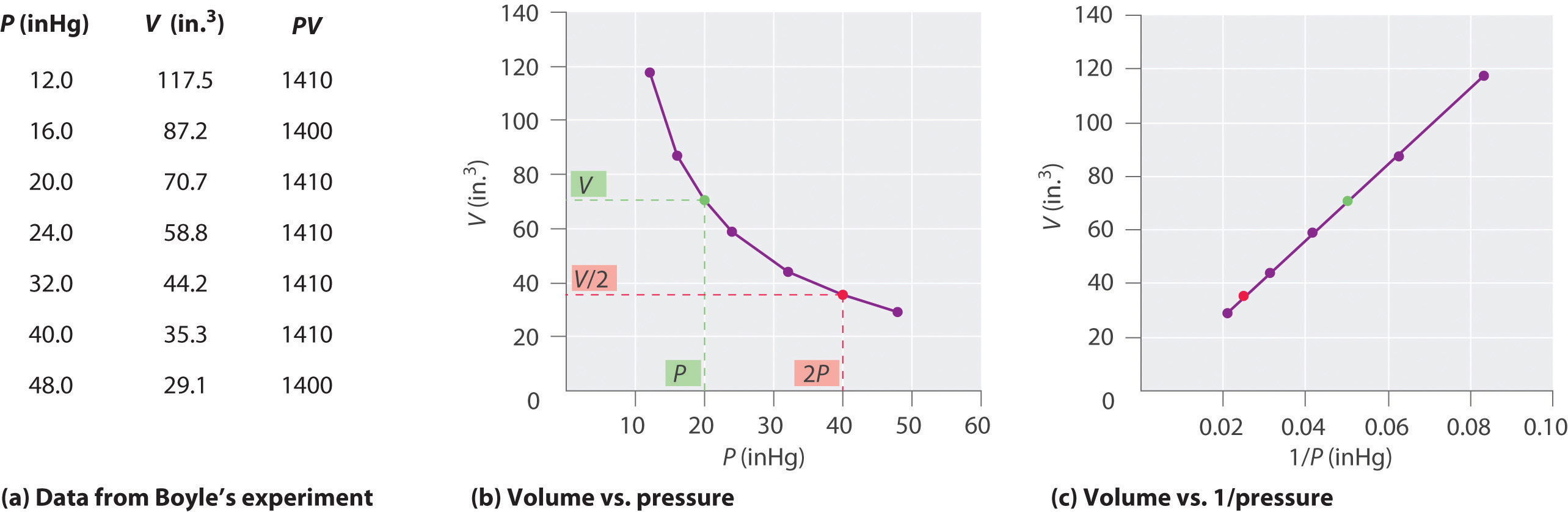
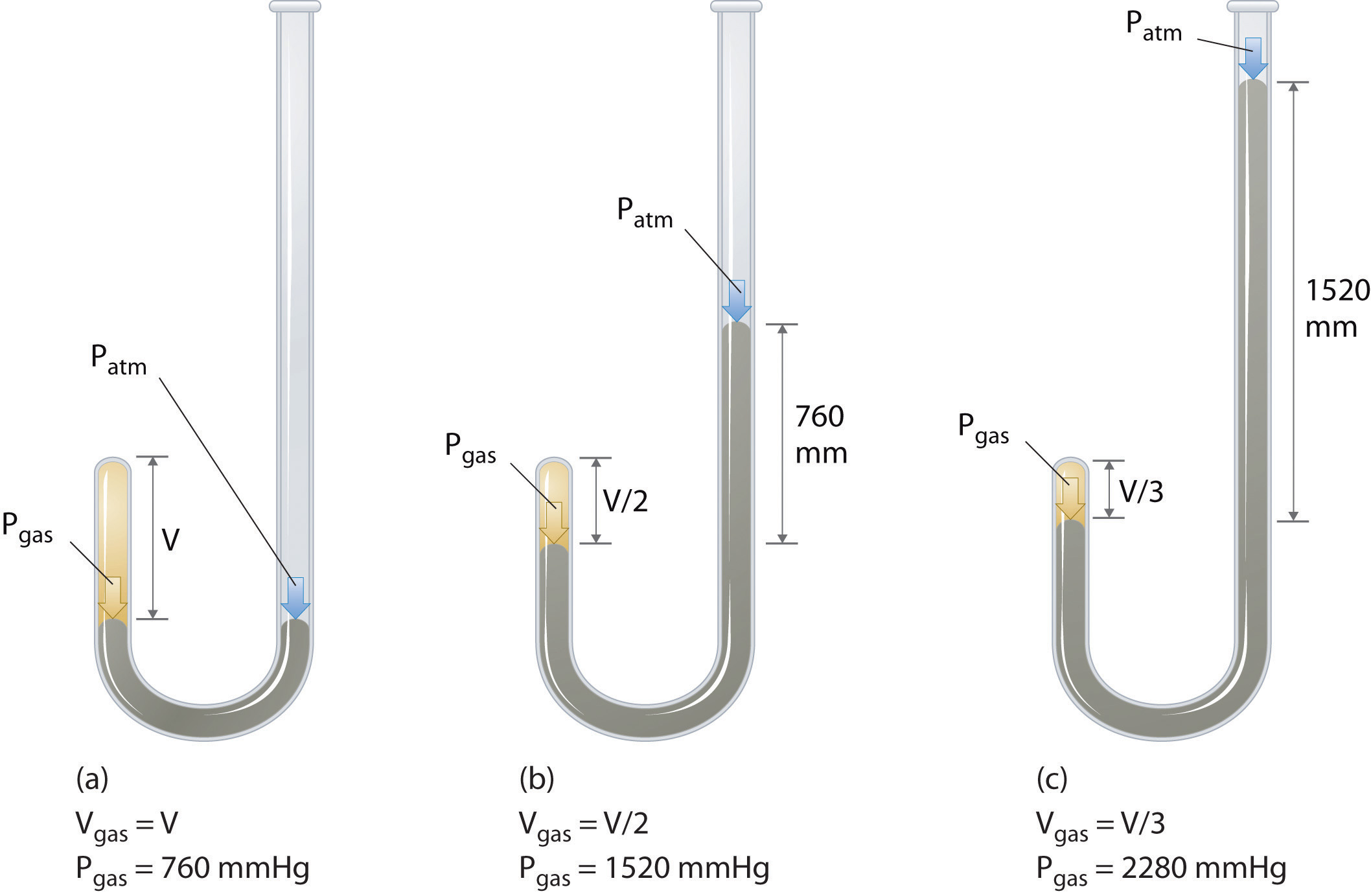
Le chimiste Irlandais Robert Boyle (1627-1691) réalisé certaines des premières expériences qui ont déterminé la relation quantitative entre la pression et le volume d’un gaz. Boyle a utilisé un tube en forme de J partiellement rempli de mercure, comme le montre la Figure \(\PageIndex{1}\)., Dans ces expériences, une petite quantité de gaz ou d’air est piégée au-dessus de la colonne de mercure et son volume est mesuré à pression atmosphérique et à température constante. Plus de mercure est ensuite versé dans les bras ouvert pour augmenter la pression sur l’échantillon de gaz. La pression sur le gaz est la pression atmosphérique plus la différence de hauteur des colonnes de mercure, et le volume résultant est mesuré. Ce processus est répété jusqu’à ce qu’il n’y ait plus de place dans le bras ouvert ou que le volume du gaz soit trop petit pour être mesuré avec précision., Des données telles que celles d’une des propres expériences de Boyle peuvent être tracées de plusieurs manières (Figure \(\PageIndex{2}\)). Un graphique simple de \(V\) versus \(P\) donne une courbe appelée hyperbole et révèle une relation inverse entre la pression et le volume: lorsque la pression est doublée, le volume diminue d’un facteur deux. Cette relation entre les deux grandeurs est décrite comme suit:
\
en Divisant les deux côtés par \(P\) donne une équation illustrant la relation inverse entre \(P\) et \(V\):
\
ou
\
où l’ ∝ symbole est lu « est proportionnelle à.” Un tracé de V versus 1 / P est donc une droite dont la pente est égale à la constante de l’équation 6.2.1 et de l’équation 6.2.3. La division des deux côtés de L’équation 6.2.1 par V au lieu de P donne une relation similaire entre P et 1 / V., La valeur numérique de la constante dépend de la quantité de gaz utilisée dans l’expérience et de la température à laquelle les expériences sont réalisées. Cette relation entre pression et volume est connue sous le nom de loi de Boyle, d’après son découvreur, et peut être énoncée comme suit: à température constante, le volume d’une quantité fixe d’un gaz est inversement proportionnel à sa pression.