Finden der quadratischen Funktionen für gegebene Parabeln – Quadratische Funktionen

Finden der quadratischen Funktionen für gegebene Parabeln

Es gibt so viele verschiedene Arten von Problemen, die Sie in Bezug auf quadratische Gleichungen stellen können. In diesem Artikel wird der Fokus darauf gelegt, wie wir eine quadratische Gleichung aus einem quadratischen Graphen mit verschiedenen Methoden entwickeln können., Aber bevor wir uns mit solchen Problemen befassen, nehmen Sie sich einen Moment Zeit, um mit quadratischen Ausdrücken auf diesem wunderbaren Online-Grafikrechner hier herumzuspielen. Je komfortabler Sie mit quadratischen Grafiken und Ausdrücken sind, desto einfacher wird dieses Thema!

Lassen Sie uns nun Probleme mit diesem Wissen lösen, nämlich wie man die Gleichung einer Parabel findet!

So finden Sie eine quadratische Gleichung aus einem Diagramm:

Um eine quadratische Gleichung aus einem Diagramm zu finden, gibt es zwei einfache Methoden, die man anwenden kann: mit 2 Punkten oder mit 3 Punkten.,

1) Finde quadratische Gleichung aus 2 Punkten

Um eine quadratische Gleichung aus einem Graphen mit nur 2 Punkten zu finden, muss einer dieser Punkte der Scheitelpunkt sein. Mit dem Scheitelpunkt und einem anderen Punkt können wir diese Koordinaten in die sogenannte „Scheitelpunktform“ unterteilen und dann für unsere Gleichung lösen., Die Scheitelpunktformel ist wie folgt, wobei (d,f) der Scheitelpunkt und (x,y) der andere Punkt ist:

(y±d)=a(x±f)2(y \pm d) = a(x \pm f)^{2}(y±d)=a(x±f)2

Scheitelpunktform kann auch in ihre Form geschrieben werden mehr „richtige“ Form, als:

y=a(x±f)2∓dy = a(x \pm f)^{2} \mp dy=a(x±f)2∓d

Mit dieser Formel müssen wir nur den Scheitelpunkt und den anderen Punkt subieren, für a lösen und dann unsere endgültige Gleichung neu schreiben., Der beste Weg, sich mit der Verwendung dieses Formulars vertraut zu machen, besteht darin, ein Beispielproblem damit zu machen.

Beispiel:

Bestimmen Sie die Gleichung der Parabel, die im Bild unten gezeigt wird.

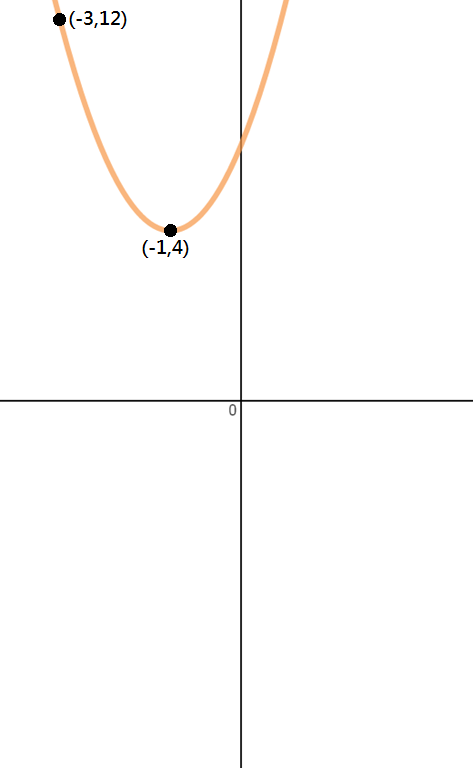
Schritt 1: Identifizieren Sie Punkte

Da wir bei diesem Problem nur zwei Punkte erhalten, den Scheitelpunkt und einen anderen Punkt, müssen wir das Scheitelpunktformular verwenden, um löse diese Frage.,

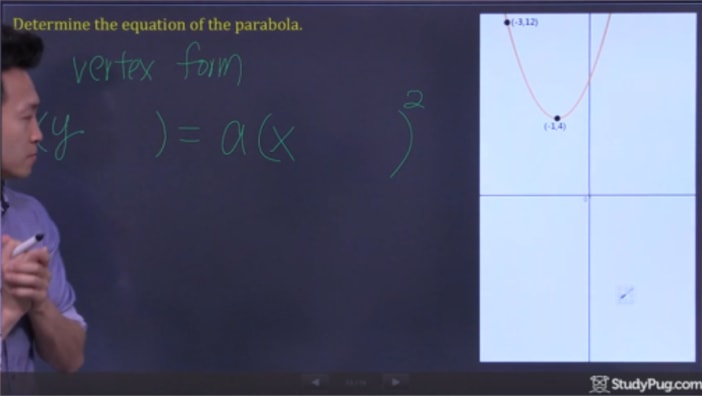
Schritt 2: Sub Punkte In Vertex Form und Lösen für „a“

Jetzt alle wir haben zu tun ist sub in unsere zwei punkte in die Scheitelpunktformel und lösen für „a“, um alle Informationen zu haben, um unsere endgültige quadratische Gleichung zu schreiben.,4)=ein(-3+1)2(12 – 4) = ein(-3 + 1)^{2}(12-4)=a(-3+1)2

8=a(-2)28 = a(-2)^{2}8=a(-2)28=4a8 = 4a8=4aa=2a = 2a=2

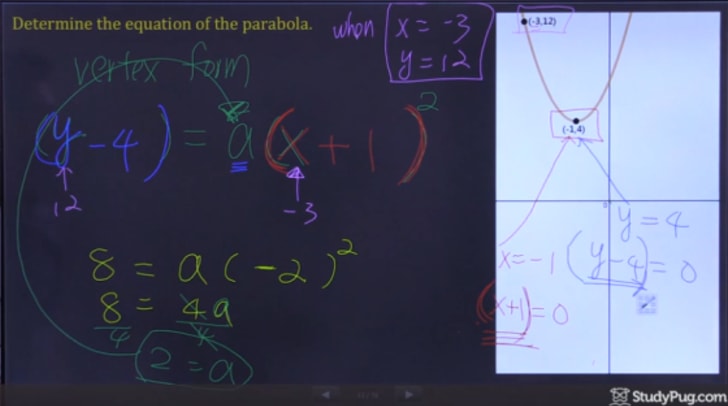
Schritt 3: Schreiben Sie die Quadratische Gleichung

Nach der Lösung für „ein“ wir haben jetzt alle Informationen, die wir brauchen, um schreiben unsere endgültige Antwort.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

Und dann, in der richtigen vertex form einer Parabel, unsere endgültige Antwort:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

Das ist die Lektion auf der Scheitelpunkt-form und so finden Sie eine quadratische Gleichung von der 2-Punkte!, Wenn Sie Ihr Gedächtnis zu verwandten Themen auffrischen möchten, z. B. Wie man quadratische Ausdrücke in Scheitelpunktform löst, wie man eine reguläre quadratische Gleichung von Standardform in Scheitelpunktform konvertiert, indem man das Quadrat vervollständigt, und wie man Scheitelpunktformel verwendet, sollten Sie sich unsere Lektionen ansehen.

2) Finde quadratische Gleichung von 3 Punkten

In einigen Fällen haben wir nicht so viel Glück, den Punkt auf dem Scheitelpunkt zu erhalten. Wenn dies der Fall ist, können wir den quadratischen Ausdruck nicht mehr mit nur zwei Punkten finden und müssen etwas anderes tun., Für den Fall, dass wir Informationen über die x-Intercepts einer Parabel sowie einen anderen Punkt erhalten, können wir die quadratische Gleichung unter Verwendung einer Gleichung finden, die als „faktorisierte Form“bezeichnet wird. Die allgemeine Gleichung für die faktorisierte Formularformel lautet wie folgt, wobei b und c die x-Koordinatenwerte der x-Intercepts sind:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

Mit dieser Formel müssen wir nur die x-Koordinatenwerte eingeben.-koordinaten der x-Intercepts, ein weiterer Punkt, und dann lösen für eine so können wir unsere endgültige Antwort schreiben., Auch hier ist der beste Weg, um sich mit dieser Form von quadratischen Gleichungen vertraut zu machen, ein Beispielproblem.

Beispiel:

Bestimmen Sie die Gleichung der Parabel im Bild unten gezeigt:

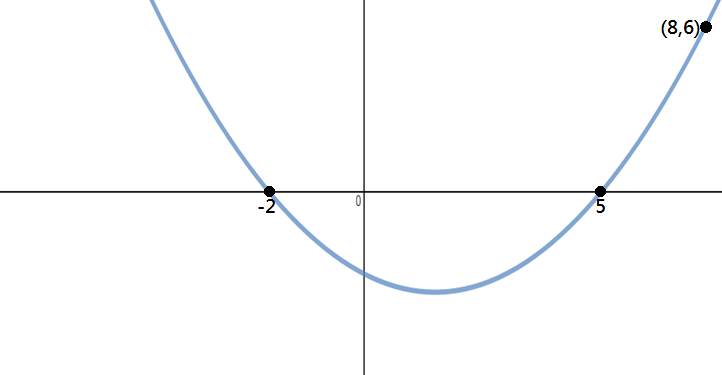
Schritt 1: Identifizieren Punkte

Da wir drei Punkte in diesem Problem erhalten, die x-Intercepts und einen anderen Punkt, können wir factored Form verwenden, um diese Frage zu lösen.,

Aus dem Graphen können wir sehen, dass die x-Intercepts -2 und 5 sind und der Punkt auf der Parabel (8,6) ist.

Schritt 2: Unterpunkte in Scheitelpunktform und Lösen für“a“

Jetzt müssen wir nur noch unsere Werte in die faktorisierte Formularformel unterteilen und lösen für „a“ um alle Informationen zu haben, um unsere endgültige quadratische Gleichung zu schreiben.,(x – 5)y=(x+2)(x−5)

Neben, wir können mit dem Punkt auf der Parabel (8,6) zu lösen, „a“:

6=a(8+2)(8-5)6 = ein(8 + 2)(8 – 5)6=a(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30aa=15 a = \frac{1}{5}a=51

Schritt 3: Schreiben Sie die Quadratische Gleichung

Nach der Lösung für „ein“ wir haben jetzt alle Informationen, die wir brauchen, um schreiben unsere endgültige Antwort.,

y – =15(x+2)(x−5)y = \frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

Und das ist alles dort ist zu ihm! Dies sind die beiden wichtigsten Methoden, um eine quadratische Funktion aus einer bestimmten Parabel zu finden. Weitere Studien zu quadratischen Funktionen und ihren Graphen finden Sie in diesen nützlichen Videos, die sich mit Diskriminanten, grafischen quadratischen Ungleichungen und konischen Abschnitten befassen.