Bayesin lause löytää monia käyttötarkoituksia todennäköisyyslaskenta ja tilastot. On pieni mahdollisuus, että et ole koskaan kuullut tästä teoreemasta elämässäsi. Osoittautuu, että tämä lause on löytänyt tiensä maailmaan koneoppimisen, muodostaa yksi erittäin koristeltu algoritmeja. Tässä artikkelissa, opimme kaikki naiivi Bayes algoritmi, sekä sen muunnelmia eri tarkoituksiin koneoppiminen.
Kuten arvata saattoi, tämä vaatii meitä näkemään asioita todennäköisyysperusteinen näkökulmasta., Aivan kuten koneoppimisessa, meillä on attribuutteja, vastemuuttujia ja ennusteita tai luokituksia. Käyttämällä tätä algoritmia, voimme olla tekemisissä todennäköisyys jakaumat muuttujat aineisto ja ennustaa todennäköisyys, että vastemuuttuja kuuluvat tiettyyn arvoon, ottaen huomioon ominaisuudet uusi esiintymä. Aloitetaan tarkastelemalla Bayesin teoreemaa.
Bayesin lause
tämän avulla voidaan tarkastella tapahtuman todennäköisyyttä perustuen etukäteen saatuun tietoon mistä tahansa entiseen tapahtumaan liittyvästä tapahtumasta., Siis esimerkiksi todennäköisyys, että hinta talo on korkea, voidaan arvioida paremmin, jos tiedämme, mitä palveluita sen ympärille, verrattuna arviointi on tehty ilman tietoa sijainti talon. Bayesin lause tekee juuri niin.

Edellä yhtälö antaa perus edustus Bayesin lause., Tässä A ja B ovat kaksi tapahtumaa, ja
P(A|B) : ehdollinen todennäköisyys, että tapahtuma A tapahtuu , kun otetaan huomioon, että B on tapahtunut. Tätä kutsutaan myös posterioriseksi todennäköisyydeksi.
P(A) ja P(B) : todennäköisyys A ja B välittämättä toisistaan.
P(B / A) : ehdollinen todennäköisyys , että tapahtuma B tapahtuu, koska A on tapahtunut.
nyt katsotaan, miten tämä sopii hyvin koneoppimisen tarkoitukseen.,
Ottaa yksinkertainen kone oppimisen ongelma, jossa meidän täytyy oppia meidän malli tietyn joukon ominaisuuksia(koulutus esimerkkejä) ja sitten muodostaa hypoteesi, tai liittyen vastemuuttuja. Sitten käytämme tätä suhdetta ennustamaan vastausta, kun otetaan huomioon uuden instanssin ominaisuudet. Bayesin teoreemaa käyttäen sen avulla voidaan rakentaa oppija, joka ennustaa johonkin luokkaan kuuluvan vastemuuttujan todennäköisyyden, kun otetaan huomioon uudet attribuutit.
harkitse edellistä yhtälöä uudelleen. Nyt, olettaa, että A on vastemuuttuja ja B on input attribuutti., Joten mukaan yhtälö, meillä on
P(A|B) : ehdollinen todennäköisyys, että vastemuuttuja kuuluvat tiettyyn arvoon, koska input-attribuutteja. Tätä kutsutaan myös posterioriseksi todennäköisyydeksi.
P(A) : vastemuuttujan ennakkotodennäköisyys.
P(B) : koulutustietojen tai todisteiden todennäköisyys.
P(B|A) : Tätä kutsutaan todennäköisyyttä koulutuksen tiedot.,
näin Ollen, yllä oleva yhtälö voidaan kirjoittaa muotoon
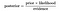
otetaanpa ongelma, jossa useita attribuutteja on yhtä suuri kuin n, ja vastaus on boolean-arvo, eli se voi olla yksi kaksi luokkaa. Myös attribuutit ovat kategorisia (2 kategoriaa tapauksessamme). Nyt, kouluttaa luokittaja, meidän on laskettava P (B|A), kaikki arvot tapauksessa ja vaste tilaa., Tämä tarkoittaa, meidän täytyy laskea 2 * (2^n -1), parametrit oppimisen tämän mallin. Tämä on selvästi epärealistista useimmilla käytännön oppimisalueilla. Jos esimerkiksi boolilaisia ominaisuuksia on 30, meidän on arvioitava yli 3 miljardia parametria.
Naiivi Bayes Algoritmi
monimutkaisuus edellä Bayes-luokittelija on vähennettävä, jotta se olisi käytännöllinen. Naiivi Bayes-algoritmi tekee sen tekemällä oletuksen ehdollisesta riippumattomuudesta koulutustietokantaan nähden. Tämä vähentää huomattavasti edellä mainitun ongelman monimutkaisuutta vain 2n.,
olettaen, ehdollinen riippumattomuus toteaa, että koska satunnaismuuttujat X, Y ja Z, sanomme että X on ehdollisesti riippumaton Y, koska Z, jos ja vain jos todennäköisyysjakauman ekp: n X on riippumaton Y: n arvo annetaan Z.
Toisin sanoen, X ja Y ovat ehdollisesti riippumattomia annettuna Z, jos ja vain jos annettu tieto, että Z tapahtuu, tieto siitä, onko X tapahtuu, ei tarjoa tietoa todennäköisyyttä Y tapahtuu, ja tieto siitä, onko Y tapahtuu säädetään, ei tietoa todennäköisyys, että X tapahtuu.,
Tämä oletus tekee Bayes algoritmi, naiivi.
ottaen Huomioon, n eri määritteiden arvot todennäköisyys, nyt voidaan kirjoittaa
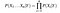
Tässä X edustaa ominaisuuksia tai ominaisuuksia, ja Y on vastemuuttuja. Nyt, P (X / Y) tulee yhtä suuri kuin tuotteet, todennäköisyysjakauma kunkin ominaisuuden X annettu Y.,
Maksimoi Jälkikäteen
Mistä olemme kiinnostuneita, on löytää posterior todennäköisyys tai P(Y|X). Nyt, useita arvoja Y, meidän täytyy laskea tämän ilmaisun kunkin niistä.
Koska uusi esiintymä Xnew, meidän täytyy laskea todennäköisyys, että Y saa ottaa mikä tahansa arvo, koska on havaittu, määritteen arvot Xnew ja koska jakaumat P(Y) ja P(X|Y) arvioida koulutuksen tiedot.
Niin, miten voimme ennustaa luokan vastemuuttuja, joka perustuu eri arvoja me saavutamme P(Y|X)., Otamme yksinkertaisesti kaikkein todennäköisin tai suurin näistä arvoista. Siksi tämä menettely tunnetaan myös posteriorin maksimoimisena.
Maksimoida Todennäköisyys
Jos oletetaan, että vastemuuttuja on tasaisesti jakautunut, että on yhtä todennäköistä saada mitään vastausta, sitten voimme edelleen yksinkertaistaa algoritmi. Tällä oletuksella priori eli P(Y) muuttuu vakioarvoksi, joka on 1/vasteen luokat.
Kuten, priori ja todisteet ovat nyt riippumattomia vastemuuttuja, nämä voidaan poistaa yhtälöstä., Siksi posteriorin maksimointi vähenee todennäköisyysongelman maksimoimiseksi.
Ominaisuus Jakelu
Kuten edellä, meidän täytyy arvioida, jakelu vastemuuttuja koulutuksesta asettaa tai oletetaan tasainen jakauma. Samoin, arvioida parametrit ominaisuus on jakelu, täytyy olettaa, jakelu tai luo-parametriset mallit on koulutus asetettu. Tällaisia oletuksia kutsutaan tapahtumamalleiksi. Näiden oletusten vaihtelut synnyttävät erilaisia algoritmeja eri tarkoituksiin., Jatkuvissa jakaumissa Gaussin naiivi Bayes on valinnan algoritmi. Diskreeteille ominaisuuksille monikansalliset ja Bernoulli jakaantuvat suosituiksi. Yksityiskohtaiset keskustelut näistä muutoksista eivät kuulu tämän artiklan soveltamisalaan.
naiivit Bayes-luokittajat toimivat mutkikkaissa tilanteissa todella hyvin yksinkertaistetuista oletuksista ja naiiviudesta huolimatta. Etu nämä luokittelijoita on, että ne vaativat pieni määrä koulutusta tietoja arvioitaessa parametrit tarpeen luokittelu. Tämä on algoritmi valinta tekstin luokitteluun., Tämä on perusajatus naiivien Bayes luokittelijat, että sinun täytyy alkaa kokeilla algoritmia.