Löytää quadratic toiminnot koska paraabelien – toisen Asteen Toiminnot

Löytää Quadratic Toiminnot Koska Paraabelien

On niin monia erilaisia ongelmia, voit olla pyysi suhteen toisen asteen yhtälöt. Tässä artikkelissa keskitytään siihen, miten voimme kehittää quadratic yhtälö, quadratic kaavio käyttäen pari eri menetelmiä., Mutta, ennen kuin pääsemme tämäntyyppisiä ongelmia, ota hetki pelata noin quadratic ilmaisuja tämä ihana online kuvaaja laskin täällä. Mitä mukavampi olet quadratic kaavioita ja ilmaisuja, sitä helpompaa tämä aihe on!

Nyt päästä ratkaisemaan ongelmia tämän tiedon, eli miten löytää yhtälö paraabelin!

Miten Löytää toisen Asteen Yhtälö Kuvaaja:

jotta löytää toisen asteen yhtälö kuvaaja, on olemassa kaksi yksinkertaisia menetelmiä voidaan käyttää: käyttämällä 2 pistettä, tai käyttämällä 3 pistettä.,

1) Löytää toisen Asteen Yhtälö 2 Pistettä

jotta löytää toisen asteen yhtälö kuvaajan käyttämällä vain 2 pistettä, yksi niistä pistettä on otettava, piste. Kanssa huippupiste ja yksi muu kohta, voimme sub näitä koordinaatteja, mitä kutsutaan ”huippupiste muodossa” ja sitten ratkaista meidän yhtälö., Vertex kaava on seuraava, jos (d,f) on vertex-piste ja (x,y) on toinen seikka:

(y±d)=a(x±f)2(y \pm d) = (x \pm f)^{2}(y±d)=a(x±f)2

Vertex muodossa voi myös olla kirjoitettu sen enemmän ”oikea” muoto, kuten:

y=a(x±f)2∓dy = a(x \pm f)^{2} \mp dy=a(x±f)2∓d

Käyttämällä tätä kaavaa, kaikki meidän täytyy tehdä, on osa vertex ja toinen kohta, ratkaista, ja sitten kirjoittaa meidän lopullinen yhtälö., Paras tapa tulla mukavaksi käyttämällä tätä lomaketta on tehdä esimerkkiongelma sen kanssa.

Esimerkki:

Määrittää yhtälön paraabelin kuvassa alla.

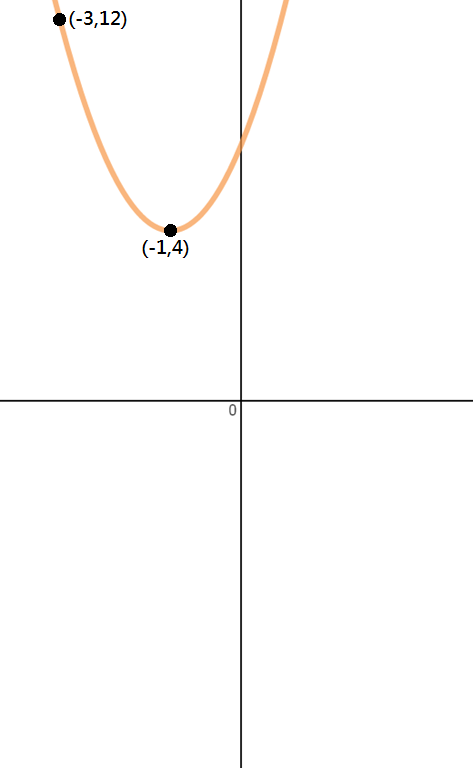
Askel 1: Tunnista Pistettä

Koska me annetaan vain kaksi pistettä tässä ongelma, vertex ja toinen kohta, meidän täytyy käyttää vertex muodossa ratkaista tämä kysymys.,

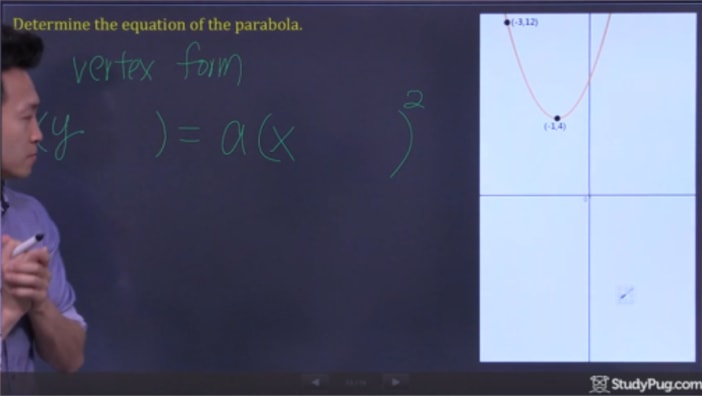
Vaihe 2: Osa Pistettä Osaksi Vertex Muodossa ja Ratkaista ””

Nyt kaikki meidän täytyy tehdä, on osa meidän kaksi pistettä kärki kaava ja ratkaista ”” saada kaikki tiedot, kirjoittaa meidän lopullinen asteen yhtälö.,4)=a(-3+1)2(12 – 4) = a(-3 + 1)^{2}(12-4)=a(-3+1)2

8=(-2)28 = (-2)^{2}8=(-2)28=4a8 = 4a8=4aa=2 a = 2 a=2

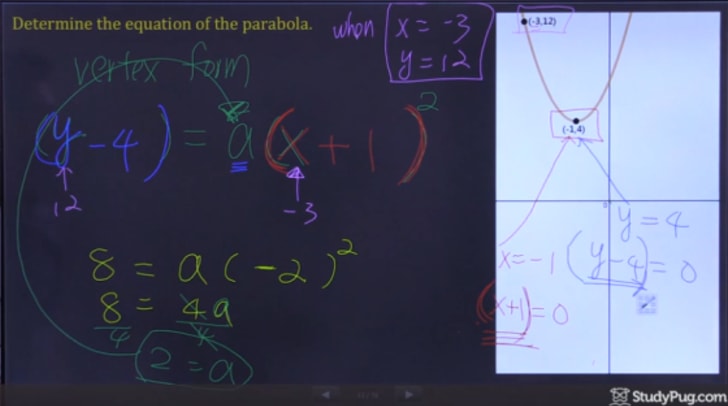
Vaihe 3: Kirjoittaa toisen Asteen Yhtälö

ratkaisemisen Jälkeen ”a”, meillä on nyt kaikki tiedot, meidän täytyy kirjoittaa ulos meidän lopullinen vastaus.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2} – y−4=2(x+1)2

Ja sitten, oikea vertex muodostaa paraabelin, meidän lopullinen vastaus on:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

Joka täydentää oppiaiheen vertex muodossa ja miten löytää toisen asteen yhtälö 2 pistettä!, Jos haluat muistin virkistämiseksi liittyviä aiheita kuten, miten ratkaista toisen asteen ilmaisuja vertex muodossa, miten muuntaa säännöllinen toisen asteen yhtälö vakio muodossa vertex muodossa täyttämällä neliön, ja miten käyttää vertex kaava, varmista, tutustu oppitunteja.

2) Etsi Quadratic yhtälö 3 pistettä

joissakin tapauksissa, emme ole niin onnekas, että annetaan kohta, huippupiste. Jos näin on, emme voi enää löytää toisen asteen ilmaisua käyttäen vain kaksi pistettä, ja täytyy tehdä jotain hieman erilaista., Siinä tapauksessa, että meille annetaan tietoa x-kuuntelevansa paraabeli, sekä yksi muu kohta, voimme löytää toisen asteen yhtälö käyttämällä yhtälö, joka on nimeltään ”järjestelmällisesti muodossa”. Yleinen yhtälö huomioon muodossa kaava on seuraava, b ja c on x-koordinaatti arvot x-kuunteluja:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

Käyttämällä tätä kaavaa, kaikki meidän täytyy tehdä, on osa x-koordinaatit x-kuuntelevansa, toinen kohta, ja sitten ratkaista niin, että voimme kirjoittaa meidän lopullinen vastaus., Jälleen, paras tapa saada mukava tämän muodon quadratic yhtälöt on tehdä esimerkki ongelma.

Esimerkki:

Määrittää yhtälön paraabelin kuvassa alla:

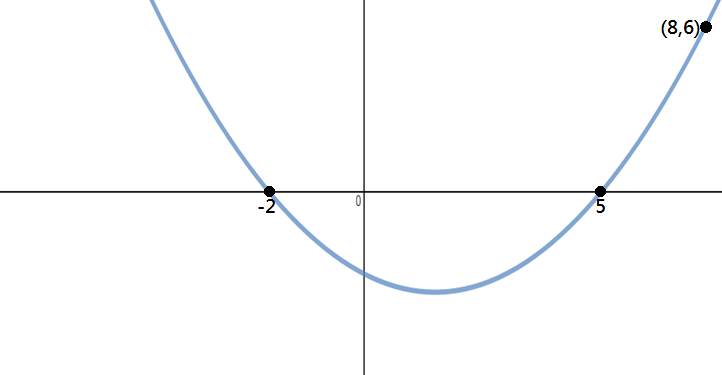
Askel 1: Tunnistaa Pistettä

Koska me annetaan kolme pistettä tässä ongelma, x-kuuntelevansa ja toinen kohta, voimme käyttää huomioon lomakkeen ratkaista tämä kysymys.,

kuvaajasta näkyy, että x-interceptit ovat -2 ja 5, ja paraabelin piste on (8,6).

Vaihe 2: Sub Pistettä Osaksi Vertex Muodossa ja Ratkaista ””

Nyt kaikki meidän täytyy tehdä, on osa meidän arvot huomioon lomakkeen kaavan ja ratkaista ”” saada kaikki tiedot, kirjoittaa meidän lopullinen asteen yhtälö.,(x – 5)y=(x+2)(x−5)

Seuraava, voimme käyttää piste paraabeli (8,6) ratkaista ”a”:

6=a(8+2)(8-5)6 = a(8 + 2)(8 – 5)6=a(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30aa=15 a = \frac{1}{5}a=51

Vaihe 3: Kirjoittaa Asteen Yhtälön

ratkaisemisen Jälkeen ”a”, meillä on nyt kaikki tiedot, meidän täytyy kirjoittaa ulos meidän lopullinen vastaus.,

y=15(x+2)(x−5)y = \frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

Ja siinä kaikki siellä on se! Nämä ovat kaksi tärkeintä menetelmiä löytää quadratic funktio tietyn parabola. Edelleen tutkimus quadratic toiminnot ja niiden kuvaajat, tarkista nämä hyödyllisiä videoita, joissa käsitellään erotteluanalyysi, piirtäminen toisen asteen eriarvoisuutta, ja conic jaksoissa.