kolmiulotteisia Muotoja: Monitahokkaan, Kaareva kuiva ja Pinta-Ala

Tämä sivu tutkitaan ominaisuuksia kolmiulotteinen tai ’solid’ muotoja.

kaksiulotteisella muodolla on pituutta ja leveyttä. Kolmiulotteisessa kiinteässä muodossa on myös syvyyttä. Kolmiulotteisia muotoja, luonteeltaan, on sisäpuoli ja ulkopuoli, erotettu pinta. Kaikki fyysiset esineet, joihin voi koskea, ovat kolmiulotteisia.,

Tämä sivu kattaa sekä suora-puolinen kiintoaineen kutsutaan monitahokkaan, jotka perustuvat polygoneja, ja kiintoaineen käyrät, kuten pallot, sylinterit ja käpyjä.

Monitahokkaan

Monitahokkaan (tai polyhedra) ovat suora-puolinen kiinteitä muotoja. Monitahokkaan perustuvat polygoneja, kaksi ulotteinen kone muotoja, suoria viivoja.

katso sivulta monikulmioiden Ominaisuudet Lisää polygonien kanssa työskentelystä.

Monitahokkaan on määritelty seuraavasti:

• Suorat reunat.
• litteät sivut, joita kutsutaan kasvoiksi.,
• kulmat, joita kutsutaan verticeiksi.

Monitahokkaan ovat myös usein määritelty lukumäärä, reunat, kasvot ja kärjet he ovat, sekä onko heidän kasvonsa ovat sama muoto ja koko. Kuten polygoneja, monitahokkaan voi olla säännöllinen (perustuu säännölliset monikulmiot) tai epäsäännöllisiä (perustuu epäsäännöllinen polygoneja). Monitahokkaat voivat olla myös koveria tai kuperia.

yksi perus-ja tutuimmista monitahokkaista on kuutio. Kuutio on säännöllinen monitahokas, ottaa kuuden neliön kasvot, 12 reunat, ja kahdeksan kärjet.,

Säännöllisen Monitahokkaan (Platoninen Kiintoaineita)

viisi säännöllinen kiinteät aineet ovat erityisen luokan monitahokkaan, jonka kaikki kasvot ovat identtiset, jossa jokainen kasvot on säännöllinen monikulmio. Platonin kiintoaineita ovat:

• Tetraedri, jossa on neljä kolmion kasvot.
• kuutio, jossa on kuusi neliönmuotoista naamaa.
• oktaedri, jossa on kahdeksan tasasivuista kolmiopintaa.
• dodekaedri kahdellatoista Pentagonin kasvolla.
• ikosaedri kahdellakymmenellä tasasivuisella kolmiopinnalla.,

Katso kaavio yllä esimerkki jokainen näistä säännöllisen monitahokkaan.

Mikä on Prisma?

Prisma on mikä tahansa monitahokas, jolla on kaksi vastaavaa päätä ja litteät sivut. Jos leikkaa prisman missä tahansa pituudeltaan, yhdensuuntaisesti päädyn kanssa, sen poikkileikkaus on sama-päädyttäisiin kahteen Prismaan. Prisman sivut ovat parallelograms-nelisivuisia muotoja, joissa on kaksi paria sivuja, joiden pituus on yhtä suuri.

Antiprismat muistuttavat tavallisia prismoja, niiden päät täsmäävät., Kuitenkin sivut anti-prismat koostuvat kolmioista eikä parallelograms. Antiprismoista voi tulla hyvin monimutkaisia.

mikä on pyramidi?

pyramidi on monitahokas, jonka monikulmioinen pohja yhdistyy kärkipisteeseen, jonka sivut ovat suorat.

Vaikka meillä on tapana ajatella pyramidit kanssa neliö pohja, kuten ne, jotka muinaiset Egyptiläiset rakennettu, ne voivat itse asiassa olla mikä tahansa monikulmion pohja, säännöllinen tai epäsäännöllinen. Lisäksi pyramidi voi olla apex suoraan keskustaan sen pohja, Oikea Pyramidi, tai voi olla apex pois keskustasta, kun se on Vino Pyramidi.,

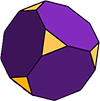
Monimutkaisempia Monitahokkaan

On olemassa monia muitakin polyhedra: symmetrinen ja epäsymmetrinen, kovera ja kupera.

esimerkiksi Arkhimedealaiset kiintoaineet koostuvat ainakin kahdesta erilaisesta säännöllisestä monikulmiosta.

typistetty kuutio (kuten kuvitettu) on Arkhimedialainen kiinteä aine, jolla on 14 kasvoa. 6 tahkoista on säännöllisiä oktagoneja ja loput 8 ovat säännöllisiä (tasasivuisia) kolmioita. Muoto on 36 reunat ja 24 vertices (kulmat).,

kolmiulotteisia Muotoja ja Käyrät

Kiinteät muodot, jotka ovat kaarevia tai pyöreä reuna eivät ole monitahokkaan. Monitahokkaan voi olla vain suorat sivut.

monet ympärilläsi olevista esineistä sisältävät ainakin joitakin käyriä. Geometriassa yleisimmät kaarevat kiintoaineet ovat sylinterit, kartiot, sfäärit ja tori (monikossa torus).,

Yhteinen kolmiulotteisia Muotoja ja Käyrät:
Sylinterin	Kartio
Sylinteri on sama poikkileikkaus yhdestä päästä toiseen. Sylintereissä on kaksi samanlaista päätä joko ympyrän tai soikean. Vaikka sylinterit ovat samanlaisia, ne eivät ole prismoja, sillä prismalla on (määritelmän mukaan) parallelogram, litteät sivut.,	kartiolla on pyöreä tai soikea pohja ja apex (tai huippupiste). Kartion puoli kapenee tasaisesti kärkeen. Kartio on samanlainen pyramidi, mutta eri kuin kartio on yksi kaareva puoli ja pyöreä pohja.
Alalla	Torus
Muotoinen pallo tai globe pallo on täysin pyöreä esine. Jokainen pallon pinnalla oleva piste on yhtä suuri etäisyys pallon keskipisteeseen.,	renkaan, renkaan tai donitsin muotoinen säännöllinen rengastorus muodostuu pyörittämällä pienempää ympyrää suuremman ympyrän ympärille. Torin muoto on myös monimutkaisempi.

Pinta-Ala

sivulla pinta-alan Laskeminen kertoo, miten selvittää alueen kaksi-ulotteinen muotoja, ja sinun täytyy ymmärtää nämä perusasiat jotta voidaan laskea pinta-ala kolmiulotteisia muotoja.

kolmiulotteisille muodoille puhutaan pinta-alasta sekaannusten välttämiseksi.,

Voit käyttää tietoa alueen kaksi-ulotteinen muotoja, laskea pinta-ala kolmiulotteinen muoto, koska jokainen kasvot tai puolella on käytännössä kaksi-ulotteinen muoto.

näin ollen treenaat kunkin kasvojen alueen ja lisäät ne yhteen.

Kuten taulu-muotojen, pinta-ala vankka ilmaistaan neliön yksikköä: cm2, inches2, m2 ja niin edelleen. Lisätietoja mittayksiköistä löydät sivuiltamme mittausjärjestelmät.,

Esimerkkejä Pinta-Ala Laskelmat

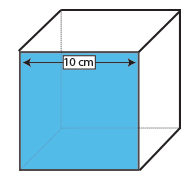
Kuutio

pinta-ala cube on alueen yksi kasvot (pituus x leveys) kerrottuna 6, koska kaikki kuusi kasvot ovat samat.

Kuten kasvot kuution on neliö, sinun tarvitsee vain ottaa yksi mittaus – pituus ja leveys neliön ovat määritelmän mukaan samat.

tämän kuution yksi kasvo on siis 10 × 10 cm = 100cm2. Kerrotaan 6, määrä kasvoja kuutiossa, ja havaitsemme, että pinta-ala tämän kuution on 600cm2.,

Muut Säännöllisen Monitahokkaan

Samalla tavalla, pinta-alan muut säännöllisen monitahokkaan (platoninen kiintoaineita) voi olla työskennellyt ulos löytää alueen toisella puolella, ja sitten kertomalla vastaus kokonaismäärä puolin – katso Perus Monitahokkaan kaavio edellä.

Jos alue on yksi pentagonin muodostavat dodekaedri on 22cm2 sitten kerro tämä kokonaismäärä puolin (12) antaa vastauksen 264cm2.,

Pyramid

laskea pinta-ala standardin pyramidi, jossa on neljä yhtä kolmion puolin ja neliön muotoinen pohja:

Ensin selvittää alueen pohja (neliö) pituus × leveys.

seuraavaksi selvitetään yhden sivun alue (kolmio). Mittaa leveys pitkin pohja ja sitten kolmion korkeus (tunnetaan myös nimellä näkökulma pituus) päässä central point pohja kärkeen.,

Voit sitten joko jakaa vastaat 2 antaa sinulle pinta-ala yksi kolmio ja sitten kerrotaan 4 antaa pinta-ala, kaikki neljä sivua, tai yksinkertaisesti moninkertaistaa pinta-ala yksi kolmio 2.

lisää lopuksi pohjan pinta-ala ja sivut yhteen löytääkseen pyramidin kokonaispinta-alan.

laskea pinta-alan muut tyypit pyramidi, lisää yhdessä alueen pohja (kutsutaan base-alue) ja alue puolin (sivusuunnassa alue), voit joutua mitata puolin erikseen.,

Nettokaaviot

geometrinen verkko on kolmiulotteisen kappaleen kaksiulotteinen ”kuvio”. Verkoista voi olla apua kolmiulotteisen kohteen pinta-alan selvittämisessä. Alla olevassa kaaviossa näet, miten peruspyramidit on rakennettu, jos pyramidi on ”aukeneva”, jäät verkkoon.

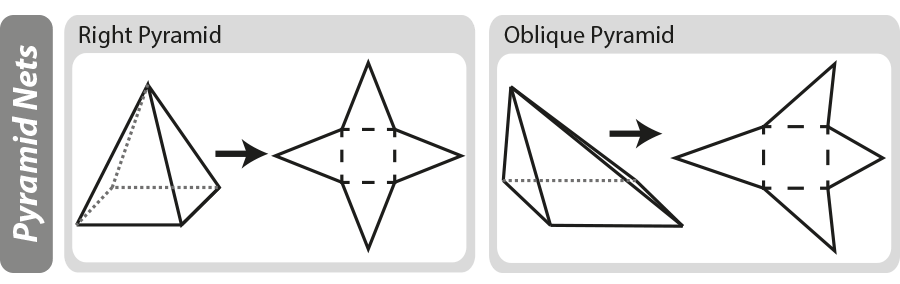
lisätietoja net kaaviot katso sivu 3D-Muotoja ja Verkot.

Prisma

laskea pinta-ala prisma:

Prismat on kaksi päättyy samalla ja tasainen puolin suunnikas.,

laske yhden pään pinta-ala ja kerro 2.

säännöllinen prisma (jossa kaikki osapuolet ovat samat) laskea alueen yksi puolin ja kerrotaan kokonaismäärä puolin.

epäsäännöllisille prismoille (eri sivuilla) lasketaan kunkin sivun pinta-ala.

Lisää kaksi vastaustasi yhteen (päät × sivut) prisman kokonaispinta-alan löytämiseksi.,

Sylinterin

laskea pinta-ala sylinterin, se on hyödyllistä miettiä osien muoto. Kuvittele purkki sokerimaissia – siinä on yläosa ja pohja, jotka molemmat ovat ympyröitä. Jos leikkaat sivun pituuttaan pitkin ja litistät sen, sinulla olisi suorakulmio. Siksi sinun täytyy löytää alue kaksi ympyrää ja suorakulmion.

treenaa ensin jonkin ympyrän pinta-ala.

ympyrän pinta-ala on π(pi) × radius2.,

Olettaen, että säde on 5cm, alue yksi piireissä on 3.14 × 52 = 78.5cm2.

Kerrotaan vastaus 2, koska on olemassa kaksi ympyrää 157cm2

ala puolella oleva sylinteri on kehä ympyrä × korkeus sylinteri.

kehä on yhtä suuri kuin π x 2 × säde. Esimerkissämme, 3.14 × 2 × 5 = 31.4

mittaa sylinterin korkeus – esimerkiksi korkeus on 10cm. Sivun pinta-ala on 31,4 × 10 = 314cm2.,

koko pinta-ala voidaan löytää lisäämällä alan piireissä ja puoli yhteen:

157 + 314 = 471cm2

Kartio

laskettaessa pinta-ala kartion, sinun täytyy käyttää pituus ’slant’ sekä säde pohja.

Kuitenkin, se on suhteellisen helppo laskea:

pinta-ala ympyrän juuressa kartion on, π(pi) × radius2.

tässä esimerkissä summa on 3.14 × 52 = 3.14 × 25 = 78.,5cm2

– alueen puolella, viisto-osiossa, voidaan löytää käyttämällä tätä kaavaa:

π(pi) x säde x pituus näkökulma.

esimerkkimme summa on 3,14 × 5 × 10 = 157cm2.

lisää lopuksi pohja-alue sivualueelle, jotta saadaan kartion kokonaispinta-ala.

78.5 + 157 = 235.5cm2

Alalla

pinta-ala on pallo, joka on suhteellisen yksinkertainen laajentaminen kaava ympyrän pinta-ala.

4 × π × radius2.,

pallo se on usein helpompi mitata halkaisija – etäisyys koko alalla. Voit sitten löytää säde, joka on puolet halkaisija.

tavallisen tennispallon halkaisija on 2,6 tuumaa. Säde on siis 1,3 tuumaa. Kaavaan tarvitaan säde. 1.3 × 1.3 = 1.69.

pinta-ala tennispallo on siis:

4 × 3.14 × 1.69 = 21.2264 inches2.,

Torus

jotta voidaan laskea pinta-ala torus sinun täytyy löytää kaksi säde-arvot.

suuri tai suuri säde (R) on mitattu keskeltä reiän keskelle rengas.

pieni tai pieni säde (r) mitataan renkaan keskeltä ulkoreunaan.

kaaviossa on kaksi näkymää esimerkistä torus ja siitä, miten sen säteitä (tai säteitä) mitataan.,

laskelma pinta-alan löytämiseksi on kahdessa osassa (yksi kutakin sädettä kohti). Laskelma on sama jokaiselle osalle.

kaava on: pinta-ala = (2nR)(2nr)

selvittää pinta-ala esimerkiksi torus.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

Moninkertaistaa kaksi vastausta yhdessä löytää yhteensä pinta-ala esimerkiksi torus.