
lyhyt selitys ja todisteet
Järkevä Root Lause (RRT) on kätevä työkalu, on teidän matemaattisia arsenal. Se tarjoaa ja nopea ja likainen testi järkevyys joitakin ilmaisuja. Se auttaa löytämään polynomien rationaaliset juuret.,
Here ’ s how and why it works.,e53714″>
Miten
Oletetaan, että sinulla on polynomin aste n, kanssa integer kertoimia:

Järkevä Root Lause todetaan: Jos järkevä root on olemassa, sitten sen osat tulee jakaa ensimmäisen ja viimeisen kertoimia:

järkevä root on ilmaistu alhaisin., Se tarkoittaa, että p: llä ja q: lla ei ole yhteisiä tekijöitä. (Se on tärkeää myöhemmin.) Osoittaja jakaa vakion polynomin päässä; demominaattori jakaa johtavan kertoimen.
esimerkiksi:
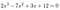
Meidän tarvitsee vain katsoa 2 ja 12.,:
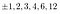
The factors of 2:
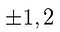
Thus, if a rational root does exist, it’s one of these:
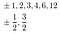
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
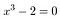
Furthermore:
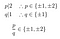
Not one of these candidates qualifies., Hypätä:
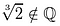
Miksi
Anna s mennä takaisin meidän paradigma polynomi.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Kerrotaan kaiken qⁿ:

Jokainen termi vasemmalla on p yhteistä. Ota se huomioon.,

Se näyttää paljon pahempi kuin se tarvitsee olla. Korvataan kaikki suluissa oleva s: llä.
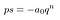
Se on paljon helpompaa silmille.
Muista, että p ja q ovat kokonaislukuja. Niillä ei myöskään ole yhteisiä tekijöitä., Siksi p ei voi jakaa qⁿ: ta. Se täytyy jakaa a₀:
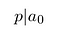
Näin ollen osoittaja jakaa jatkuva aikavälillä.
mene takaisin meidän paradigma polynomi:

Tällä kertaa, huono ensimmäinen termi oikealla puolella.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
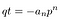
Again, q and p have no common factors. Therefore:
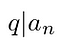
Thus proves the rational root theorem.