Calculate Log & Antilog Online (Suomi)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

Missä

• b = base,
• y = numero,
• x = log arvo.

Laskeminen Antilog:

y = 10x

Missä

• x = numero,
• y = antilog arvo.

Logaritmit ja Anti-Logaritmit: Miten Se Toimii ja Sen Merkitys

– Opas Kirjoittanut Sin ’ B. Arenas, joka julkaistiin 1. lokakuuta 2019

Jos olet koskaan miettinyt, miten asiantuntijat määrittää pitkiäkin matkoja, maanjäristys intensiteetti, ja maailmantalouden kasvu hinnat, sitten olet tullut oikeaan paikkaan.

hyvin suurten summien laskeminen voi olla hidasta ja hämmentävää., Logaritmien (log) ja antilogaritmien (antilog) avulla laskutoimitukset voidaan kuitenkin tehdä yksinkertaisemmiksi.

Lue lisää logista ja antilogista, miten ne toimivat ja miksi nämä ovat merkityksellisiä matemaattisia käsitteitä.

mikä on logaritmi?

A logaritmi on se voima, jonka numero (kutsutaan base) on kerrottava, jotta itse saada tietty määrä. Yksinkertaisemmin logaritmi ratkaisee ongelman:

kuinka monta kertaa kerrotaan b, jotta saadaan toinen numero y?,

logaritmi laskee, kuinka monta kertaa sama tekijä on kerrottava saavuttaakseen tietyn luvun.

kuka sen keksi?

Log keksittiin 1500-luvulla skotlantilaisen matemaatikon, fyysikon ja tähtitieteilijän John Napierin laskentavälineeksi. Hän kirjoitti kirjan Mirifici Logarithmorum Canonis descriptio taulukoita ja numeroita keskustella luonnolliset logaritmit, jossa vahvistetaan pohjaa sen perusajatus.

Napier termin logaritmi kreikan sanasta logos, joka tarkoittaa ’suhde tai osuus,’ ja arithmos, joka tarkoittaa numero.,’Yhdistettynä se tarkoittaa kirjaimellisesti’ suhdelukua.’

2 eri Logaritmit

luonnollinen logaritmi numero on sen kirjautuu alustaan vakio e, missä e on suunnilleen sama kuin 2.718281828459. Yhtälö kirjoitetaan muodossa loge (x).

Jos logaritmi ei määrittele emästä, kuten tämä esimerkki: log(1000), se tunnetaan yleisenä logaritmina, joka käyttää emästä 10.

log(1000), se tunnetaan yleisenä logaritmina, joka käyttää emästä 10.

miten Logia käytetään?,

Kun aloitat laskemalla luvut miljoonia, miljardeja ja biljoonia, se voi saada varsin verottamalla. Onko kyseessä laskenta paljon rahaa, kasvu väestön, tai kattaa pitkiä matkoja, loki voi työskennellä sinulle. Se voi yksinkertaistaa suuria summia, joihin liittyy pitkiä ja hämmentäviä yhtälöitä, mikä helpottaa niiden ymmärtämistä.

Tässä on standardi yhtälö log:
logb(x) = y,

Missä

• numero kerrottuna itsellään (b) on pohja.
• kerrottujen kertojen määrä (y) on logaritmi.,
• saatu luku (x) kirjoitetaan suluissa.

ymmärtää, miten konsepti toimii, tässä on esimerkki, jossa pienempi numero:
Kysymys: Kuinka monta 2s me moninkertaistaa saada 32?
b = 2, x = 32

log2(32) = y
Vastaus: 2 x 2 x 2 x 2 x 2 = 32,

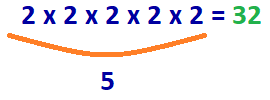
5 useita 2s on kerrottava, jotta saadaan numero 32.
vastaus: log2(32) = 5,

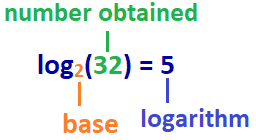
näin Ollen, tässä esimerkki: logaritmi 32 base 2 on 5, tai 2-kantainen logaritmi 32 on 5.,

lisäksi log on eksponentiaation käänteisfunktio, jossa matemaattinen operaatio kirjoitetaan bn. b on emäs, joka kerrotaan n: n voiman mukaan, joka on kerrottujen kertojen määrä itselleen.

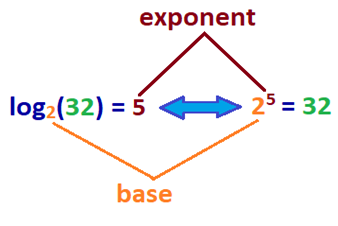
Mitä tämä tarkoittaa? Luvun loki on eksponentti, johon base b kerrotaan tietyn luvun saamiseksi. Voit antaa sinulle paremman idean, katso näyte log yhtälö asetettu rinnalla sen eksponentiaalinen yhtälö alla.,

kirjaudu	eksponentti
log2(32) = 5	25 = 32

Nyt kokeillaan useita.
Kysymys: Kuinka monta 10s me moninkertaistaa saada 150,000,000,000?
b = 10, x = 150,000,000,000

logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.,1760912590557

tämä ratkaistaan tieteellisen laskurin lokifunktion avulla. Tai käytä tämän sivun laskinta saadaksesi vastauksen.

miten Antilogaritmi liittyy Logiin?

loki numero voi sitten palautetaan sen alkuperäinen numero. Tämä voidaan tehdä käyttämällä antilogaritmia (antilog). Näin antilogi on login käänteisfunktio. Samoin antilog toimii eksponentoida yksinkertaistettu log arvo.,

laskea antilog useita y, sinun täytyy nostaa logaritmi pohja b (yleensä 10, joskus jatkuva e) voima, joka tuottaa määrän y.

Tässä on yhtälö antilog käyttäen pohja 10:
10 x = y
Missä x on eksponentti-ja y on antilog arvo.

esimerkiksi, jos otamme tämän yhtälön, log(5) = x, sen antilog on 10x = 5.

• Loki: loki(5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

Nyt kokeillaan sitä suurempi numero.,

Jos otamme log(150,000,000,000) = x, sen antilog on 10x = 150,000,000,000.

• Kirjaudu: log10(150,000,000,000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150,000,000,000

Tärkeä, ja reaalimaailman Sovelluksia

Ennen keksinnön laskimet, logaritmit käytettiin yksinkertaistaa laskelmia eri aloilla tietämyksen, kuten navigointi, maanmittaus, tähtitiede, ja myöhemmin, suunnittelu.

Kuvittele purjehdusta keskellä ei mitään 1500-luvulla., Silloiset Suunnistajat luottivat tähtien sijaintiin ja sekstanttimekanismiin selvittääkseen niiden tarkan sijainnin. Ilman modernia teknologiaa, joka auttaa laskemaan pitkiä matkoja, voit käyttää logia laskelmien yksinkertaistamiseen. Tarkkuus on tärkeää, tai riskeeraat useampia päiviä merellä niukoilla Tarvikkeilla. Vähemmän yhtälöitä tarkoittaa vähemmän tilaa virheille.

entä muut käytännön sovellukset? Elävän tieteen mukaan logaritmit liittyvät geometrisiin progressioihin aritmeettisiin progressioihin., Jos olet koskaan huomannut toistuvia muotoja ja kuvioita luonto, arkkitehtuuri ja taide, nämä muodostumat hallussaan omia vastaava logaritminen arvoja.

nykyään tieto siitä, miten nämä kuviot toimivat, vaikuttaa siihen, miten ihmiskunta rakentaa ja suunnittelee taloja, rakennuksia ja kaupunkimaisemia.

logaritmeja käytetään myös ilmaisemaan tiettyjen asteikkojen laajuutta ja voimakkuutta., Lisäksi laaja etäisyydet, ja suurilla nopeuksilla, se mittaa muita asioita, kuten:

• Äänen voimakkuus
• Äänen taajuus
• Voimaan myrskyjen
• Voimaa maanjäristyksiä
• Syövyttäviä taso happojen
• Kovuus mineraaleja,
• Kirkkaus tähdet

otetaan desibeliä esimerkkinä. Jotta kaiuttimet kovenevat 10 desibelillä, se on toimitettava 10-kertaisella teholla. Kun lisäät sen +20 dB, se tarvitsee 100 kertaa teho, ja +30 dB se tarvitsee 1000 teho.

lisäksi äänen voimakkuus etenee aritmeettisesti., Se muuttuu myös suhteessa geometrisesti etenevän ääniaallon logaritmiin.

Alla on taulukko, Live Tiede listaus eri logaritminen asteikot vastaavat lineaariset asteikot.

Mittaamaan Hinnat ja Riveissä

Mukaan Kalid Azad, matematiikka kouluttaja takana BetterExplained.com, logaritmit ovat, miten me selvittää, miten nopeasti jotain kasvaa.

yhteiset logaritmit kuvaavat periaatteessa lukuja niiden potenssiin 10. Korkojen osalta logaritmi on Sijoituksen kasvu.,

määritettäessä maan BKT: n kasvuvauhtia analyytikot arvioivat bruttokansantuotetta seuraavina vuosina. Ne ottavat edellisen vuoden BKT: n ja seuraavan vuoden BKT: n, sitten laskevat logaritmin löytääkseen arvioidun kasvuvauhdin.

hakukoneet käyttävät linkin kaavio auttaa pisteet merkitystä, luotettavuus & viranomaisen asiakirjoja kautta web. Googlen PageRank oli merkittävä kehitys haussa, joka lisäsi hakurelevanssia ja auttoi Google search marketshare.,

Mukaan Azad, asteikolla 1-10, aloitussivun, jossa on PageRank 2 on 10 kertaa enemmän suosittu kuin sivun PageRank 1. Jos sivusto on PageRank 5 ja kilpailija-sivusto on PageRank 9, niin se on ero 4 suuruusluokkaa.

suuruusjärjestys tarkoittaa karkeasti 10x eroa, tai sijoitus on 1 numero suurempi verrattuna toiseen. Tässä tapauksessa sivuston PageRank 9 on 100,000,000 suositumpi kuin sivuston PageRank-1.,

Rivi

Kirjaudu ja antilog ovat merkittäviä, tietojenkäsittelyn menetelmiä, joiden avulla voimme yksinkertaistaa suuria summia. Yksinkertaistaminen lyhentää laskentaprosessia ja helpottaa laskelmien ymmärtämistä. Tämä auttaa vähentämään tilaa virheille.

Lisäksi, käyttäen log tarjoaa mitattavissa asteikot mitata luonnollinen ilmiö, kuten maanjäristys intensiteetti, voima myrskytuulet, ja kirkkautta tähtiä. Rahoituksen osalta logaritmit antavat meille mahdollisuuden paikantaa korkoja ja talouskasvua.

sitä käytetään käytännössä monilla aloilla., Mittaustarkkuudesta riippuvat suuret arvot hyötyvät logaritmisista laskelmista.

Author

Sin ’ on innokas tutkija ja kirjailija taloudellisia aiheita—opiskelu suhdanteet, miten ne vaikuttavat väestön, sekä miten auttaa kuluttajia tekemään viisaampia taloudellisia päätöksiä. Hänen muita artikkeleita voidaan lukea Inquirer.net ja Manileno.com. Hänellä on Maisterin tutkinto Luova Kirjoittaminen Yliopistosta Filippiinit, yksi alkuun akateemisten instituutioiden maailmassa, ja Kandidaatin Viestintä Arts Miriam College.