momento de inercia, forma general
dado que el momento de inercia de un objeto ordinario implica una distribución continua de la masa a una distancia que varía continuamente de cualquier eje de rotación, el cálculo de momentos de inercia generalmente implica el cálculo, la disciplina de las matemáticas que puede manejar tales variables continuas., Dado que el momento de inercia de una masa puntual se define por
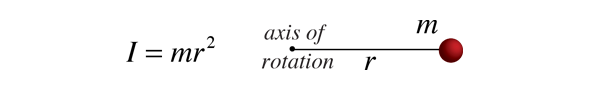
entonces el momento de inercia contribución por un elemento de masa infinitesmal dm tiene la misma forma. Este tipo de elemento de masa se denomina elemento diferencial de masa y su momento de inercia viene dado por

tenga en cuenta que el elemento diferencial de momento de inercia dI siempre debe definirse con respecto a un eje de rotación específico., La suma sobre todos estos elementos de masa se llama una integral sobre la masa.
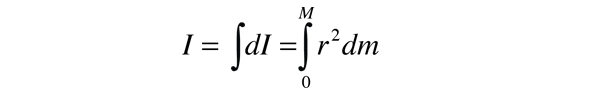
generalmente, el elemento de masa dm se expresará en términos de la geometría del objeto, de modo que la integración se pueda llevar a cabo sobre el objeto como un todo (por ejemplo, sobre una barra larga uniforme).
habiendo llamado a esto una forma general, es probablemente apropiado señalar que es una forma general solo para ejes que pueden ser llamados «ejes principales», un término que incluye todos los ejes de simetría de objetos., El concepto de momento de inercia para objetos generales sobre ejes arbitrarios es un tema mucho más complicado. El momento de inercia en tales casos toma la forma de una cantidad tensórica matemática que requiere nueve componentes para definirla completamente.
| Ejemplos de integración para obtener el momento de inercia. | varilla Recta |
| Cilindro | |
| Esfera |