El teorema de Bayes encuentra muchos usos en la teoría de la probabilidad y la estadística. Hay una posibilidad de que nunca hayas oído hablar de este teorema en tu vida. Resulta que este teorema ha encontrado su camino en el mundo del aprendizaje automático, para formar uno de los algoritmos altamente decorados. En este artículo, aprenderemos todo sobre el algoritmo Bayes ingenuo, junto con sus variaciones para diferentes propósitos en el aprendizaje automático.
como habrás adivinado, esto requiere que veamos las cosas desde un punto de vista probabilístico., Al igual que en el aprendizaje automático, tenemos atributos, variables de respuesta y predicciones o clasificaciones. Usando este algoritmo, vamos a tratar con las distribuciones de probabilidad de las variables en el conjunto de datos y predecir la probabilidad de la variable de respuesta que pertenece a un valor particular, dados los atributos de una nueva instancia. Comencemos revisando el teorema de Bayes.
Teorema de Bayes
Esto nos permite examinar la probabilidad de un evento basado en el conocimiento previo de cualquier evento relacionado con el anterior evento., Así, por ejemplo, la probabilidad de que el precio de una casa es alta, se puede evaluar mejor si conocemos las instalaciones a su alrededor, en comparación con la evaluación hecha sin el conocimiento de la ubicación de la casa. El teorema de Bayes hace exactamente eso.

Ecuación anterior da básicas de representación del teorema de Bayes., Aquí A y B son dos eventos y,
P (A / B) : la probabilidad condicional de que ocurra el evento a , dado que B ha ocurrido. Esto también se conoce como la probabilidad posterior.
P (A) Y P ( B): probabilidad de A y B sin tener en cuenta el uno del otro.
P (B / A): la probabilidad condicional de que ocurra el evento B , dado que a ha ocurrido.
Ahora, vamos a ver cómo esto se adapta bien al propósito del aprendizaje automático.,
tomemos un simple problema de aprendizaje automático, donde necesitamos aprender nuestro modelo de un conjunto dado de atributos(en ejemplos de entrenamiento) y luego formar una hipótesis o una relación con una variable de respuesta. Luego usamos esta relación para predecir una respuesta, dados los atributos de una nueva instancia. Usando el teorema de Bayes, es posible construir un alumno que predice la probabilidad de que la variable de respuesta pertenezca a alguna clase, dado un nuevo conjunto de atributos.
Considere la ecuación anterior de nuevo. Ahora, supongamos que A es la variable de respuesta y B es el atributo de entrada., Así que de acuerdo con la ecuación, tenemos
P(A|B) : probabilidad condicional de variable de respuesta perteneciente a un valor particular, dados los atributos de entrada. Esto también se conoce como la probabilidad posterior.
P (A): la probabilidad previa de la variable de respuesta.
P (B): la probabilidad de datos de entrenamiento o la evidencia.
P (B / A) : esto se conoce como la probabilidad de los datos de entrenamiento.,
por lo Tanto, la ecuación anterior puede escribirse como
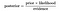
Vamos a echar un problema, donde el número de atributos es igual a n, y la respuesta es un valor booleano, es decir, puede estar en una de las dos clases. Además, los atributos son categóricos (2 categorías para nuestro caso). Ahora, para entrenar el clasificador, necesitaremos calcular P (B / A), para todos los valores en el espacio de instancia y respuesta., Esto significa que tendremos que calcular 2 * (2^n -1), parámetros para aprender este modelo. Esto es claramente poco realista en la mayoría de los dominios de aprendizaje práctico. Por ejemplo, si hay 30 atributos booleanos, entonces necesitaremos estimar más de 3 mil millones de parámetros.
algoritmo Bayes ingenuo
la complejidad del clasificador Bayesiano anterior debe reducirse, para que sea práctico. El algoritmo de Bayes ingenuo hace eso haciendo una suposición de independencia condicional sobre el conjunto de datos de entrenamiento. Esto reduce drásticamente la complejidad del problema mencionado anteriormente a solo 2n.,
el supuesto de independencia condicional establece que, dadas las variables aleatorias X, Y Y Z, decimos Que X es condicionalmente independiente de y dado Z, si y solo si la distribución de probabilidad que gobierna X es independiente del valor de y dado Z.
En otras palabras, X e y son condicionalmente independientes dado Z si y solo si, dado el conocimiento de que z ocurre, el conocimiento de si x ocurre no proporciona información sobre la probabilidad de que ocurra Y, y el conocimiento de si ocurre Y no proporciona información sobre la probabilidad de que ocurra X.,
Esta suposición hace que el algoritmo Bayes, ingenuo.
Dado, n diferentes valores de atributo, la probabilidad de ahora puede ser escrito como
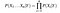
Aquí, X representa los atributos o características, y y es la variable de respuesta. Ahora, P (X|Y) se convierte en igual a los productos de, distribución de probabilidad de cada atributo X dado Y.,
maximizando a Posteriori
lo que nos interesa es encontrar la probabilidad posterior O P (Y / X). Ahora, para múltiples valores de Y, necesitaremos calcular esta expresión para cada uno de ellos.
dada una nueva instancia Xnew, necesitamos calcular la probabilidad de que y tome cualquier valor dado, dados los valores de atributos observados de Xnew y dadas las distribuciones P(Y) Y P(X / y) estimadas a partir de los datos de entrenamiento.
entonces, ¿cómo vamos a predecir la clase de la variable de respuesta, basado en los diferentes valores que alcanzamos para P (Y / X)., Simplemente tomamos el más probable o máximo de estos valores. Por lo tanto, este procedimiento también se conoce como maximización a posteriori.
maximización de la verosimilitud
si asumimos que la variable de respuesta está distribuida uniformemente, es decir, es igualmente probable que obtenga cualquier respuesta, entonces podemos simplificar aún más el algoritmo. Con esta suposición el priori o P(y) se convierte en un valor constante, que es 1/categorías de la respuesta.
como, los priori y la evidencia son ahora independientes de la variable de respuesta, Estos pueden ser eliminados de la ecuación., Por lo tanto, la maximización a posteriori se reduce a maximizar el problema de probabilidad.
distribución de características
como se ha visto anteriormente, necesitamos estimar la distribución de la variable de respuesta del conjunto de entrenamiento o asumir una distribución uniforme. Del mismo modo, para estimar los parámetros para la distribución de una entidad, se debe asumir una distribución o generar modelos no paramétricos para las entidades a partir del conjunto de entrenamiento. Tales supuestos se conocen como modelos de eventos. Las variaciones en estos supuestos generan diferentes algoritmos para diferentes propósitos., Para distribuciones continuas, el gaussiano naive Bayes es el algoritmo de elección. Para características discretas, distribuciones multinomiales y Bernoulli como populares. La discusión detallada de estas variaciones está fuera del alcance de este artículo.
los clasificadores Bayes ingenuos funcionan muy bien en situaciones complejas, a pesar de las suposiciones simplificadas y la ingenuidad. La ventaja de estos clasificadores es que requieren un pequeño número de datos de entrenamiento para estimar los parámetros necesarios para la clasificación. Este es el algoritmo de elección para la categorización de texto., Esta es la idea básica detrás de los clasificadores Bayes ingenuos, que necesita comenzar a experimentar con el algoritmo.