
Una breve explicación y prueba
La Raíz Racional Teorema (TSR) es una herramienta muy útil para tener en su arsenal matemático. Proporciona una prueba rápida y sucia para la racionalidad de algunas expresiones. Y ayuda a encontrar raíces racionales de polinomios.,
he Aquí cómo y por qué funciona.,e53714″>
Cómo
Supongamos que usted tiene un polinomio de grado n, con coeficientes enteros:

La Raíz Racional Teorema establece que: Si una raíz racional existe, a continuación, sus componentes se divide el primer y el último coeficientes:

La raíz racional se expresa en términos mínimos., Eso significa que p y q no comparten factores comunes. (Eso será importante más adelante.) El numerador divide la constante al final del polinomio; el demominador divide el coeficiente principal.
Como un ejemplo:
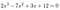
sólo hay que mirar a los 2 y los 12.,:
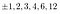
The factors of 2:
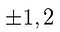
Thus, if a rational root does exist, it’s one of these:
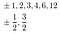
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
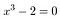
Furthermore:
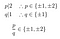
Not one of these candidates qualifies., Saltar a:
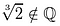
Qué
Vamos a volver a nuestro paradigma polinomio.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Multiplicar todo por qⁿ:

Cada término de la izquierda tiene p en común. Factor que fuera.,

Se parece mucho peor de lo que debe ser. Vamos a reemplazar todas esas cosas entre paréntesis con una S. realmente no nos importa lo que hay ahí.
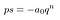
Que es mucho más fácil en los ojos.
recuerde que p y q son enteros. Tampoco comparten factores comunes., Por lo tanto, p no puede dividir q q. Se debe dividir a₀:
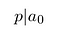
por Lo tanto, el numerador se divide el término constante.
Ahora, volvamos a nuestro paradigma polinomio:

Esta vez, la mala, el primer término del lado derecho.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
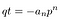
Again, q and p have no common factors. Therefore:
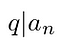
Thus proves the rational root theorem.