esta página examina las propiedades de las formas tridimensionales o «sólidas».
Una forma bidimensional tiene longitud y anchura. Una forma sólida tridimensional también tiene profundidad. Las formas tridimensionales, por su naturaleza, tienen un interior y un exterior, separados por una superficie. Todos los elementos físicos, las cosas que se pueden tocar, son tridimensionales.,
esta página cubre tanto sólidos de lados rectos llamados poliedros, que se basan en polígonos, como sólidos con curvas, como globos, cilindros y conos.
poliedros
los poliedros (o poliedros) son formas sólidas de lados rectos. Los poliedros se basan en polígonos, formas planas bidimensionales con líneas rectas.
consulte nuestra página Propiedades de polígonos para obtener más información sobre cómo trabajar con polígonos.
los poliedros se definen como:
- bordes rectos.
- lados planos llamados caras.,
- esquinas, llamadas vértices.
los poliedros también se definen a menudo por el número de aristas, caras y vértices que tienen, así como si sus caras tienen la misma forma y tamaño. Al igual que los polígonos, los poliedros pueden ser regulares (basados en polígonos regulares) o irregulares (basados en polígonos irregulares). Los poliedros también pueden ser cóncavos o convexos.
uno de los poliedros más básicos y familiares es el cubo. Un cubo es un poliedro regular, que tiene seis caras cuadradas, 12 aristas y ocho vértices.,

Poliedros Regulares (Sólidos Platónicos)
Los cinco sólidos regulares son una clase especial de poliedros, cuyas caras son idénticas con cada cara de ser un polígono regular. Los sólidos platónicos son:
- tetraedro con cuatro caras triangulares equiláteros.
- Cubo con seis caras cuadradas.
- Octaedro con ocho caras triangulares equiláteros.
- dodecaedro con doce caras del Pentágono.
- icosaedro con veinte caras triangulares equiláteros.,
vea el diagrama de arriba para una ilustración de cada uno de estos poliedros regulares.
¿Qué es un Prisma?
un prisma es cualquier poliedro que tiene dos extremos coincidentes y lados planos. Si se corta un prisma en cualquier lugar a lo largo de su longitud, paralelo a un extremo, su sección transversal es la misma: se terminaría con dos prismas. Los lados de un prisma son paralelogramos: formas de cuatro lados con dos pares de lados con la misma longitud.
Los antiprismas son similares a los prismas regulares, sus extremos coinciden., Sin embargo los lados de anti-prismas se compone de triángulos y no paralelogramos. Los Antiprisms pueden llegar a ser muy complejos.
¿Qué es una Pirámide?
una pirámide es un poliedro con una base de polígono que se conecta a un ápice (punto superior) con lados rectos.
aunque tendemos a pensar en pirámides con una base cuadrada, como las que los antiguos egipcios construyeron, de hecho pueden tener cualquier base de polígono, regular o irregular. Además, una pirámide puede tener un ápice en el Centro directo de su base, una pirámide derecha, o puede tener el ápice fuera del centro cuando es una pirámide oblicua.,
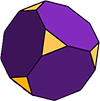
Más Complejo Poliedros
Hay muchos más tipos de poliedros: simétrica y asimétrica, cóncavas y convexas.
los sólidos de Arquímedes, por ejemplo, están formados por al menos dos polígonos regulares diferentes.
El Cubo truncado (como se ilustra) es un sólido Arquimedeo con 14 caras. 6 de las caras son octágonos regulares y los otros 8 son triángulos regulares (equiláteros). La forma tiene 36 aristas y 24 vértices (esquinas).,
las formas tridimensionales con curvas
las formas sólidas que incluyen un borde curvado o redondo no son poliedros. Los poliedros solo pueden tener lados rectos.
muchos de los objetos a su alrededor incluirán al menos algunas curvas. En Geometría los sólidos curvos más comunes son cilindros, conos, esferas y tori (el plural de torus).,
| Común de Formas Tridimensionales con Curvas: | |
|---|---|
| Cilindro | Cono |
 |
 |
| Un cilindro tiene la misma sección transversal de un extremo al otro. Los cilindros tienen dos extremos idénticos de un círculo o un óvalo. Aunque similares, los cilindros no son prismas como un prisma tiene (por definición) paralelogramo, lados planos., | un cono tiene una base circular u ovalada y un ápice (o vértice). El lado del cono se estrecha suavemente hasta el ápice. Un cono es similar a una pirámide pero distinto ya que un cono tiene un solo lado curvo y una base circular. |
| Esfera | ‘Toro’ |
 |
 |
| la Forma de una pelota o un globo, una esfera es completamente un objeto redondo. Cada punto en la superficie de una esfera está a una distancia igual al centro de la esfera., | con la forma de un anillo, un neumático o una dona, un toro anular regular se forma girando un círculo más pequeño alrededor de un círculo más grande. También hay formas más complejas de tori. |
área de superficie
nuestra página sobre calcular el área explica cómo calcular el área de las formas bidimensionales y necesita comprender estos conceptos básicos para calcular el área de superficie de las formas tridimensionales.
para las formas tridimensionales, hablamos de área de superficie, para evitar confusiones.,
Puede utilizar su conocimiento sobre el área de las formas bidimensionales para calcular el área de superficie de una forma tridimensional, ya que cada cara o lado es efectivamente una forma bidimensional.
por lo tanto, trabajar el área de cada cara, y luego sumarlas.
al igual que con las formas planas, el área de superficie de un sólido se expresa en unidades cuadradas: cm2, inches2, m2, etc. Puede encontrar más detalles sobre las unidades de medida en nuestra página sistemas de medición.,
ejemplos de cálculos de superficie
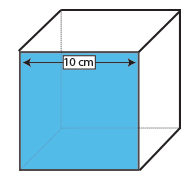
Cube
El área de superficie de un cubo es el área de una cara (longitud x Anchura) multiplicada por 6, porque las seis caras son iguales.
como la cara de un cubo es un cuadrado, solo necesita tomar una medida: la longitud y el ancho de un cuadrado son, por definición, los mismos.
Una cara de este cubo es por lo tanto 10 × 10 cm = 100cm2. Multiplique por 6, el número de caras en un cubo, y encontramos que el área de superficie de este cubo es 600cm2.,
otros poliedros regulares
de manera similar, el área de superficie de los otros poliedros regulares (sólidos platónicos) se puede calcular encontrando el área de un lado y luego multiplicando la respuesta por el número total de lados.
si el área de un pentágono que forma un dodecaedro es 22cm2, multiplique esto por el número total de lados (12) para dar la respuesta 264cm2.,
Pirámide
para calcular el área de superficie de una pirámide estándar con cuatro lados triangulares iguales y una base cuadrada:
primero calcule el área de la base (cuadrada) longitud × ancho.
siguiente calcular el área de un lado (triángulo). Mida el ancho a lo largo de la base y luego la altura del triángulo (también conocido como longitud inclinada) desde el punto central de la base hasta el ápice.,
Puede dividir su respuesta por 2 para obtener el área de superficie de un triángulo y luego multiplicar por 4 para obtener el área de superficie de los cuatro lados, o simplemente multiplicar el área de superficie de un triángulo por 2.
finalmente agregue el área de la base y los lados juntos para encontrar el área total de la superficie de la pirámide.
para calcular el área de superficie de otros tipos de pirámide, agregue el área de la base (conocida como área de base) y el área de los lados (área lateral), es posible que deba medir los lados individualmente.,
diagramas de red
una red geométrica es un ‘patrón’ bidimensional para un objeto tridimensional. Las redes pueden ser útiles al calcular el área de superficie de un objeto tridimensional. En el diagrama de abajo se puede ver cómo se construyen las pirámides básicas, si la pirámide está ‘desplegada’ se queda con la red.
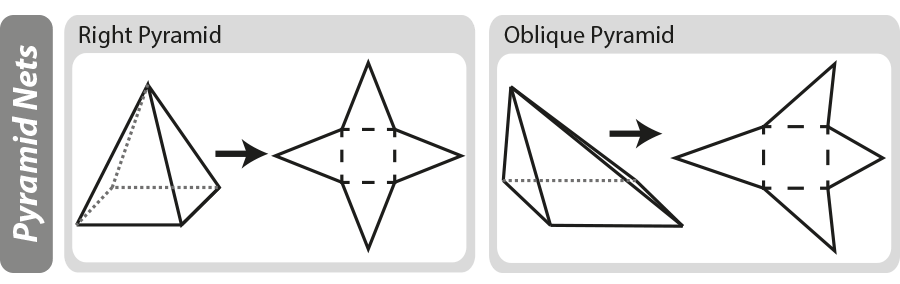
para obtener más información sobre diagramas de red, consulte nuestra página formas y redes 3D.

Prisma
para calcular el área de superficie de un Prisma:
Los prismas tienen dos extremos iguales y lados de paralelogramo planos.,
calcular el área de un extremo y multiplicar por 2.
para un prisma regular (donde todos los lados son iguales) calcular el área de uno de los lados y multiplicar por el número total de lados.
Para prismas irregulares (con diferentes lados) calcular el área de cada lado.
suma tus dos respuestas juntas (extremos × lados) para encontrar la superficie total del prisma.,
cilindro

Ejemplo:
Radio = 5cm
Altura = 10cm
para calcular la superficie de un cilindro es útil pensar en las partes componentes de la forma. Imagina una lata de maíz dulce-tiene una parte superior y una parte inferior, los cuales son círculos. Si se corta el lado a lo largo de su longitud y aplanado que tendría un rectángulo. Por lo tanto, es necesario encontrar el área de dos círculos y un rectángulo.
primero calcule el área de uno de los círculos.
el área de un círculo Es π (pi) × radius2.,
asumiendo un radio de 5cm, el área de uno de los círculos es 3.14 × 52 = 78. 5cm2.
multiplique la respuesta por 2, ya que hay dos círculos 157cm2
el área del lado del cilindro es el perímetro del círculo × la altura del cilindro.
el perímetro es igual a π x 2 × Radio. En nuestro ejemplo, 3.14 × 2 × 5 = 31.4
Mida la altura del cilindro – para este ejemplo la altura es de 10cm. La superficie del lado es 31.4 × 10 = 314cm2.,
la superficie total se puede encontrar sumando el área de los círculos y el lado juntos:
157 + 314 = 471cm2

Ejemplo:
Radio = 5cm
Longitud de inclinación = 10cm
cono
al calcular la superficie área de un cono es necesario utilizar la longitud de la ‘inclinación’, así como el radio de la base.
sin Embargo, es relativamente sencillo calcular:
El área del círculo en la base del cono es, π(pi) × radius2.
En este ejemplo, la suma es 3.14 × 52 = 3.14 × 25 = 78.,5cm2
el área del lado, la sección inclinada, se puede encontrar usando esta fórmula:
π(pi) × radio × longitud de inclinación.
en nuestro ejemplo la suma es 3.14 × 5 × 10 = 157cm2.
finalmente agregue el área base al área lateral para obtener la superficie total del cono.
78.5 + 157 = 235.5cm2

pelota de tenis:
diámetro = 2.6 pulgadas
esfera
El área de superficie de una esfera es una expansión relativamente simple de la fórmula para el área de un círculo.
4 × π × radius2.,
para una esfera a menudo es más fácil medir el diámetro – la distancia a través de la esfera. A continuación, puede encontrar el radio que es la mitad del diámetro.
El diámetro de una pelota de tenis estándar es de 2.6 pulgadas. Por lo tanto, el radio es de 1,3 pulgadas. Para la fórmula necesitamos el radio al cuadrado. 1.3 × 1.3 = 1.69.
la superficie de una pelota de tenis es por lo tanto:
4 × 3.14 × 1.69 = 21.2264 pulgas2.,

Ejemplo:
R (Radio Grande) = 20 cm
r (Radio pequeño) = 4 cm
Torus
para calcular el área de superficie de un torus, debe encontrar dos valores de radio.
el radio grande o mayor (R) se mide desde el centro del agujero hasta el centro del anillo.
el radio pequeño o menor (r) se mide desde el centro del anillo hasta el borde exterior.
el diagrama muestra dos vistas de un toro de ejemplo y cómo medir sus radios (o radios).,
el cálculo para encontrar el área de superficie está en dos partes (una para cada radio). El cálculo es el mismo para cada parte.
la fórmula es: surface area = (2NR) (2NR)
para calcular el área de superficie del Toro de ejemplo.
(2 × π × R) = (2 × 3.14 × 20) = 125.6
(2 × π × r) = (2 × 3.14 × 4) = 25.12
multiplique las dos respuestas juntas para encontrar la superficie total del Toro de ejemplo.