encontrar las funciones cuadráticas para parábolas dadas
hay tantos tipos diferentes de problemas que se le pueden preguntar con respecto a las ecuaciones cuadráticas. En este artículo, el enfoque se pondrá en cómo podemos desarrollar una ecuación cuadrática a partir de un gráfico cuadrático utilizando un par de métodos diferentes., Pero, antes de entrar en este tipo de problemas, tómese un momento para jugar con expresiones cuadráticas en esta maravillosa calculadora gráfica en línea aquí. ¡Cuanto más cómodo esté con gráficos y expresiones cuadráticas, más fácil será este tema!
Ahora vamos a resolver problemas con este conocimiento, a saber, cómo encontrar la ecuación de una parábola!
cómo encontrar una ecuación cuadrática de un gráfico:
para encontrar una ecuación cuadrática de un gráfico, hay dos métodos simples que uno puede emplear: usando 2 puntos, o usando 3 puntos.,
1) Encontrar ecuación cuadrática de 2 puntos
para encontrar una ecuación cuadrática de un gráfico usando solo 2 puntos, uno de esos puntos debe ser el vértice. Con el vértice y otro punto, podemos sub estas coordenadas en lo que se llama la «forma de vértice» y luego resolver para nuestra ecuación., La fórmula de vértice es la siguiente, donde (d,f) es el punto de vértice y (x,y) es el otro punto:
la forma de vértice también se puede escribir en su forma más «adecuada», como:
Usando esta fórmula, todo lo que necesitamos hacer es sub en el vértice y otro punto, resolver para a, y luego reescribir nuestra ecuación final., La mejor manera de sentirse cómodo con el uso de este formulario es hacer un problema de ejemplo con él.
Ejemplo:
Determinar la ecuación de la parábola que se muestra en la imagen de abajo.
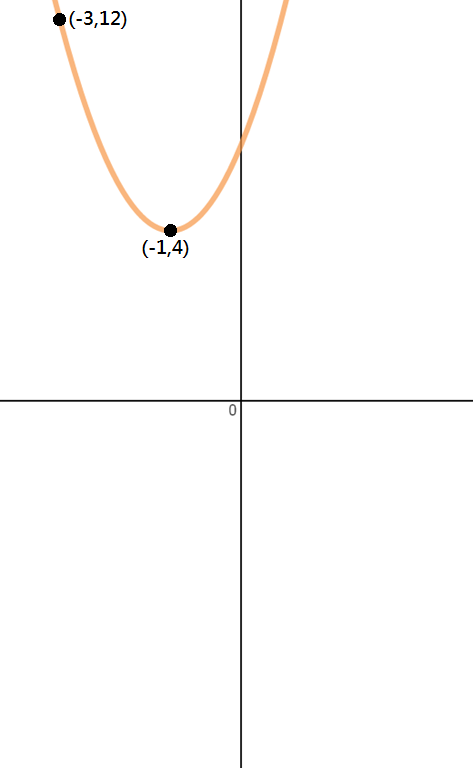
Paso 1: identificar puntos
ya que solo se nos dan dos puntos en este problema, el vértice y otro punto, debemos usar la forma de vértice para resolver esta pregunta.,
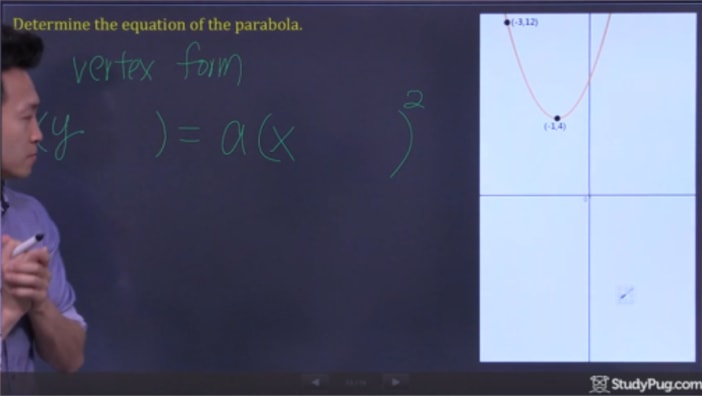
Paso 2: sub apunta en Vertex Form y resuelve para «a»
ahora todo lo que tenemos que hacer es sub en nuestros dos puntos en la fórmula de vértice y resolver para «a» para tener toda la información para escribir nuestra ecuación cuadrática final.,4)=a(-3+1)2(12 – 4) = un(-3 + 1)^{2}(12-4)=a(-3+1)2
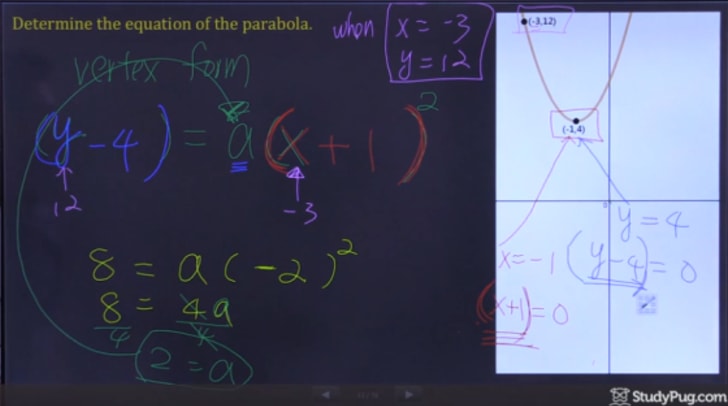
Paso 3: Escribir Ecuación Cuadrática
Después de la resolución «a», ahora tenemos toda la información que necesita para escribir nuestra respuesta final.,
Y, a continuación, en la correcta forma de vértice de una parábola, nuestra respuesta final es:
Que completa la lección en forma de vértice y cómo encontrar una ecuación cuadrática a partir de 2 puntos!, Si desea refrescar su memoria sobre los temas relacionados, como, cómo resolver expresiones cuadráticas en forma de vértice, cómo convertir una ecuación cuadrática regular de forma estándar a forma de vértice completando el cuadrado, y cómo usar la fórmula de vértice, asegúrese de revisar nuestras lecciones.
2) Encontrar ecuación cuadrática de 3 puntos
en algunos casos, no vamos a ser tan afortunados como para ser dado el punto en el vértice. Si ese es el caso, ya no podemos encontrar la expresión cuadrática usando solo dos puntos, y necesitamos hacer algo un poco diferente., En el caso de que se nos proporcione información sobre las X-interceptas de una parábola, así como otro punto, podemos encontrar la ecuación cuadrática usando una ecuación que se llama «forma factorizada». La ecuación general para la fórmula de la forma factorizada es la siguiente, con b y c siendo los valores de las coordenadas x de las intercepciones x:
Usando esta fórmula, todo lo que necesitamos hacer es sub en las coordenadas X de las intercepciones X, otro punto, y luego resolver para a para que podamos escribir nuestra respuesta final., Una vez más, la mejor manera de sentirse cómodo con esta forma de ecuaciones cuadráticas es hacer un problema de ejemplo.
ejemplo:
Determine la ecuación de la parábola que se muestra en la imagen de abajo:
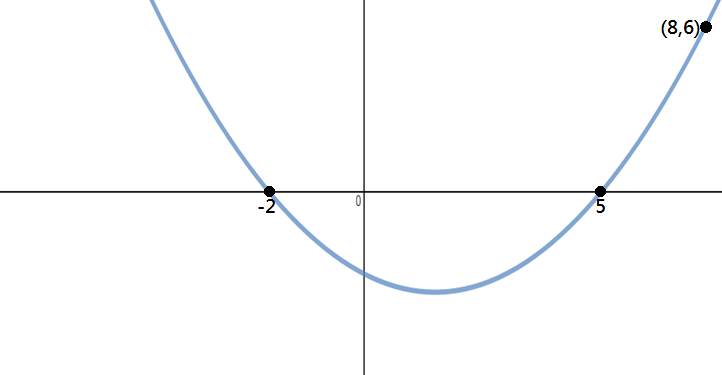
paso 1: identificar puntos
dado que se nos dan tres puntos en este problema, los x-intercepts y otro punto, podemos usar el formulario factorizado para resolver esta pregunta.,
del gráfico, podemos ver que las X-interceptas son -2 y 5, y el punto en la parábola es (8,6).
Paso 2: Sub puntos en forma de vértice y resolver para «a»
ahora todo lo que tenemos que hacer es sub en nuestros valores en la fórmula de forma factorizada y resolver para «a» para tener toda la información para escribir nuestra ecuación cuadrática final.,(x – 5)y=(x+2)(x−5)
a continuación, podemos utilizar el punto de la parábola (8,6) para solucionar de «a»:
Paso 3: Escribir Ecuación Cuadrática
Después de la resolución «a», ahora tenemos toda la información que necesita para escribir nuestra respuesta final.,
Y eso es todo lo que hay! Esos son los dos métodos más importantes para encontrar una función cuadrática de una parábola dada. Para un mayor estudio de las funciones cuadráticas y sus gráficos, echa un vistazo a estos videos útiles que tratan con el discriminante, graficando desigualdades cuadráticas y secciones cónicas.