
Log Calculator
Anti-Log Calculator
Enter the number(to the power of 10)
Select the Base value
Antilog value
Mathematical Formulas
Calculating log (logbx):
logbx = y implies by = x.,
Donde
- b = base,
- y = número
- x = log valor.
Calcular Antilog:
y = 10x
Donde
- x = número
- y = antilog valor.
logaritmos y Anti-logaritmos: cómo funciona y su importancia
– guía escrita por Corin B. Arenas, publicada el 1 de octubre de 2019
si alguna vez se ha preguntado cómo los expertos determinan las grandes distancias, la intensidad de los terremotos y las tasas de crecimiento económico global, entonces ha venido al lugar correcto.
calcular sumas muy grandes puede ser lento y confuso., Pero con la ayuda de logaritmos (log) y antilogaritmos (antilog), los cálculos se pueden hacer más simples.
siga leyendo para obtener más información sobre log y antilog, cómo funcionan y por qué estos son conceptos matemáticos relevantes.
¿Qué es el logaritmo?

un logaritmo es la potencia a la que un número (referido como la base) debe multiplicarse a sí mismo para obtener un número dado. En términos más simples, logaritmo resuelve el problema:
¿Cuántas veces multiplicamos b para obtener otro número y?,
logaritmo cuenta el número de veces que el mismo factor debe multiplicarse para llegar a un número dado.
¿A quién se le ocurrió?
Log fue inventado en el siglo XVI como una herramienta de cálculo por el matemático, físico y astrónomo escocés John Napier. Escribió El libro Mirifici Logarithmorum Canonis Descriptio con tablas y números que discuten los logaritmos naturales, sentando las bases para su concepto básico.
Napier, acuñó el término logaritmo de la palabra griega logos, que significa ‘relación o proporción,’ y arithmos que significa ‘número.,’Cuando se combina, literalmente significa’ número de razón.’
2 tipos de logaritmos
El logaritmo natural de un número es su logaritmo a la base de la constante e, donde e es aproximadamente igual a 2.718281828459. La ecuación se escribe como loge (x).
si un logaritmo no especifica una base, como este ejemplo: log (1000), se conoce como un logaritmo común que usa la base 10.
log (1000), se conoce como un logaritmo común que utiliza la base 10.
¿cómo se usa Log?,

Una vez que comience a calcular cifras por Millones, miles de millones y billones, puede ser bastante agotador. Ya sea que se trate de contar mucho dinero, el crecimiento de la población o cubrir grandes distancias, log puede funcionar para usted. Puede simplificar grandes sumas que implican ecuaciones largas y confusas, haciéndolas más fáciles de comprender.
Aquí está la ecuación estándar para log:
logb(x) = y
donde,
- El número multiplicado a sí mismo (b) es la base.
- El número de veces que se multiplica (y) es el logaritmo.,
- El número obtenido (x) se escribe entre paréntesis.
para entender cómo funciona el concepto, aquí hay un ejemplo con un número más pequeño:
Pregunta: ¿Cuántos 2s multiplicamos para obtener 32?
b = 2, x = 32
log2(32) = y
Respuesta: 2 x 2 x 2 x 2 x 2 = 32
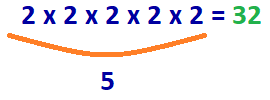
5 número 2 debe ser multiplicado para obtener el número 32.
La respuesta: log2(32) = 5
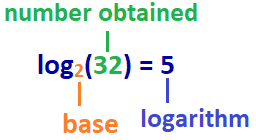
por lo tanto, en este ejemplo: el logaritmo de 32 con base 2 es 5, o log base 2 de 32 es 5.,
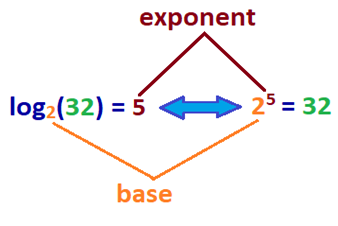
Además, log es la función inversa de la exponenciación, donde la operación matemática se escribe como bn. b es la base que se multiplica según la potencia de n, que es el número de veces que se multiplica a sí misma.
¿Qué significa esto? El registro de un número es el exponente al que se multiplica la base b Para obtener un número dado. Para darle una mejor idea, consulte la ecuación de registro de muestra junto a su ecuación exponencial a continuación.,
| registro | exponente |
|---|---|
| log2(32) = 5 | 25 = 32 |
Ahora vamos a tratar con un gran número.
Pregunta: ¿Cuántos 10s multiplicamos para obtener 150,000,000,000?
b = 10, x = 150,000,000,000
logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.,1760912590557
esto se resuelve usando la función log en una calculadora científica. O utilice la calculadora en esta página para obtener la respuesta.
¿cómo se relaciona el antilogaritmo con el registro?

un número de registro puede devolverse a su número original. Esto se puede hacer usando antilogaritmo (antilog). Por lo tanto, el antilog es la función inversa de log. Del mismo modo, antilog funciona para exponenciar un valor de registro simplificado.,
para calcular el antilog de un número y, debe elevar el logaritmo base b (Generalmente 10, a veces la constante e) a la potencia que generará el número y.
Aquí está la ecuación para antilog usando base 10:
10x = y
donde x es el exponente e y es el valor antilog.
Por ejemplo, si tomamos esta ecuación log(5) = x, su antilog será 10x = 5.
- Log: log(5) = 0.698970004336019
- Antilog: 100.698970004336019 = 5
Ahora vamos a intentarlo con un número mayor.,
Si tomamos log (150,000,000,000) = x, su antilog será 10x = 150,000,000,000.
- Log: log10(150,000,000,000) = 11.1760912590557
- Antilog: 1011.1760912590557= 150,000,000,000
importancia y aplicaciones del mundo Real

antes de la invención de las calculadoras, los logaritmos se utilizaban para simplificar los cálculos en varios campos del conocimiento, como la navegación, la topografía, la astronomía y, más tarde, la ingeniería.
Imagine navegar en medio de la nada en el siglo XVI., Los navegantes en ese entonces confiaban en la posición de las estrellas y un mecanismo sextante para determinar su ubicación exacta. Sin tecnología moderna que le ayude a calcular grandes distancias, puede usar el registro para simplificar sus cálculos. La precisión es importante, o arriesgas más días en el mar con escasos suministros. Menos ecuaciones significan menos margen de error.
¿Qué pasa con otras aplicaciones prácticas? Los logaritmos de los estados de la ciencia en vivo relacionan las progresiones geométricas con las progresiones aritméticas., Si alguna vez has notado formas y patrones repetitivos en la naturaleza, la arquitectura y el arte, estas formaciones poseen sus propios valores logarítmicos correspondientes.
hoy en día, el conocimiento de cómo funcionan estos patrones influye en la forma en que la humanidad construye y diseña casas, edificios y paisajes urbanos.
Los logaritmos también se utilizan para expresar el alcance y la intensidad de ciertas escalas., Además de grandes distancias y altas velocidades, mide otras cosas como:
- intensidad del sonido
- frecuencia del sonido
- fuerza de las tormentas de viento
- fuerza de los terremotos
- Nivel corrosivo de ácidos
- dureza de los minerales
- brillo de las estrellas
tomemos los decibelios como ejemplo. Para hacer que los altavoces sean más altos en 10 decibelios, debe suministrarse 10 veces la potencia. A medida que lo aumente a +20 dB, necesitará 100 veces la potencia, y en +30 dB necesitará 1.000 la potencia.
Además, la intensidad del sonido progresa aritméticamente., También cambia proporcionalmente con el logaritmo de una onda sonora que progresa geométricamente.
a continuación se muestra una tabla de Live Science que Lista diferentes escalas logarítmicas con sus escalas lineales correspondientes.
en la medición de tasas y rangos

según Kalid Azad, el educador de matemáticas detrás BetterExplained.com, los logaritmos son la forma de averiguar qué tan rápido está creciendo algo.
Los logaritmos comunes básicamente describen números en términos de sus potencias de 10. Cuando se trata de tasa de interés, el logaritmo es el crecimiento de una inversión.,
para determinar la tasa de crecimiento del PIB de un país, los analistas revisan el PIB en los años siguientes. Toman el PIB del año anterior y el PIB del año siguiente, luego calculan el logaritmo para encontrar la tasa de crecimiento estimada.
Los motores de búsqueda utilizan el gráfico de enlaces para ayudar a calificar la importancia, confiabilidad & Autoridad de los documentos en la web. PageRank de Google fue una evolución importante en la búsqueda que impulsó la relevancia de búsqueda y ayudó a Google marketshare de búsqueda.,
según Azad, en una escala del 1 al 10, una página de destino con un PageRank de 2 es 10 veces más popular que una página con un PageRank de 1. Si un sitio tiene un PageRank de 5, y un sitio competidor tiene un PageRank de 9, entonces tiene una diferencia de 4 órdenes de magnitud.
un orden de magnitud significa aproximadamente una diferencia de 10x, o un ranking es 1 dígito más grande en comparación con el otro. En este caso, un sitio con un PageRank 9 es 100,000,000 más popular que un sitio con PageRank 1.,
la línea de fondo
Log y antilog son métodos de computación significativos que nos permiten simplificar grandes sumas. La simplificación acorta el proceso de cálculo y hace que los cálculos sean más fáciles de comprender. Esto ayuda a reducir el margen de error.
Además, el uso de log proporciona escalas medibles para medir fenómenos naturales, como la intensidad de terremotos, la fuerza de las tormentas de viento y el brillo de las estrellas. En términos financieros, los logaritmos nos permiten identificar las tasas de interés y las tasas de crecimiento económico.
se utiliza prácticamente en muchos campos., Los grandes valores que dependen de la precisión de la medición se benefician del uso de cálculos logarítmicos.
sobre el autor
Corin es un ardiente investigador y escritor de temas financieros: estudia las tendencias económicas, cómo afectan a las poblaciones y cómo ayudar a los consumidores a tomar decisiones financieras más sabias. Sus otros artículos de fondo se pueden leer en Inquirer.net y Manileno.com tiene una Maestría en Escritura Creativa de la Universidad de Filipinas, una de las mejores instituciones académicas del mundo, y una licenciatura en Artes de la comunicación de Miriam College.