Dreidimensionale Formen: Polyeder, gekrümmte Körper und Oberfläche

Diese Seite untersucht die Eigenschaften von dreidimensionalen oder „festen“ Formen.

Eine zweidimensionale Form hat Länge und Breite. Eine dreidimensionale feste Form hat auch Tiefe. Dreidimensionale Formen haben von Natur aus ein Innen und ein Außen, getrennt durch eine Oberfläche. Alle physischen Gegenstände, Dinge, die Sie berühren können, sind dreidimensional.,

Diese Seite behandelt sowohl geradseitige Feststoffe, sogenannte Polyeder, die auf Polygonen basieren, als auch Feststoffe mit Kurven wie Globen, Zylinder und Zapfen.

Polyeder

Polyeder (oder Polyeder) sind gerade-seitige feste Formen. Polyeder basieren auf Polygonen, zweidimensionalen ebenen Formen mit geraden Linien.

Weitere Informationen zum Arbeiten mit Polygonen finden Sie auf unserer Seite Eigenschaften von Polygonen.

Polyeder sind definiert als:

• Gerade Kanten.
• Flache Seiten genannt Gesichter.,
• Ecken, sogenannte Eckpunkte.

Polyeders werden häufig auch durch die Anzahl der Kanten, Flächen und Scheitelpunkte definiert, die sie haben, sowie ob ihre Flächen alle die gleiche Form und Größe haben. Wie Polygone können Polyeder regelmäßig (basierend auf regulären Polygonen) oder unregelmäßig (basierend auf unregelmäßigen Polygonen) sein. Polyeder können auch konkav oder konvex sein.

Eines der grundlegendsten und bekanntesten Polyeder ist der Würfel. Ein Würfel ist ein reguläres Polyeder, mit sechs quadratischen Flächen, 12 Kanten und acht Eckpunkte.,

Reguläre Polyeder (platonische Festkörper)

Die fünf regulären Festkörper sind eine spezielle Klasse von Polyedern, deren Flächen alle identisch sind, wobei jede Fläche ein reguläres Polygon ist. Die platonischen Körper sind:

• Tetraeder mit vier gleichseitigen Dreiecksflächen.
• Würfel mit sechs quadratischen Flächen.
• Oktaeder mit acht gleichseitigen Dreiecksflächen.
• Dodekaeder mit zwölf pentagon Gesichter.
• Ikosaeder mit zwanzig gleichseitigen Dreiecksflächen.,

Eine Abbildung dieser regulären Polyeder finden Sie im obigen Diagramm.

Was ist ein PRISMA?

Ein Prisma ist ein beliebiges Polyeder mit zwei übereinstimmenden Enden und flachen Seiten. Wenn Sie ein Prisma irgendwo entlang seiner Länge parallel zu einem Ende schneiden, ist sein Querschnitt der gleiche-Sie würden mit zwei Prismen enden. Die Seiten eines Prismas sind Parallelogramme – vierseitige Formen mit zwei Seitenpaaren gleicher Länge.

Antiprismen ähneln regulären Prismen, ihre Enden stimmen überein., Die Seiten von Antiprismen bestehen jedoch aus Dreiecken und nicht aus Parallelogrammen. Antiprismen können sehr komplex werden.

Was ist eine Pyramide?

Eine Pyramide ist ein Polyeder mit einer Polygonbasis, die mit einer Spitze (oberer Punkt) mit geraden Seiten verbunden ist.

Obwohl wir an Pyramiden mit quadratischer Basis denken, wie sie die alten Ägypter gebaut haben, können sie tatsächlich jede Polygonbasis haben, regelmäßig oder unregelmäßig. Darüber hinaus kann eine Pyramide eine Spitze in der direkten Mitte ihrer Basis haben, eine rechte Pyramide, oder kann die Spitze in der Mitte haben, wenn es sich um eine schräge Pyramide handelt.,

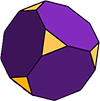
Komplexere Polyeder

Es gibt viele weitere Arten von Polyedern: symmetrisch und asymmetrisch, konkav und konvex.

Archimedische Festkörper bestehen beispielsweise aus mindestens zwei verschiedenen regulären Polygonen.

Der abgeschnittene Würfel (wie abgebildet) ist ein archimedischer Körper mit 14 Flächen. 6 der Flächen sind regelmäßige Achtecke und die anderen 8 sind regelmäßige (gleichseitige) Dreiecke. Die Form hat 36 Kanten und 24 Ecken).,

Dreidimensionale Formen mit Kurven

Feste Formen, die eine gekrümmte oder runde Kante enthalten, sind keine Polyeder. Polyeder können nur gerade Seiten haben.

Viele der Objekte um Sie herum enthalten mindestens einige Kurven. In der Geometrie sind die gebräuchlichsten gekrümmten Feststoffe Zylinder, Kegel, Kugeln und Tori (der Plural für Torus).,

Gemeinsame Dreidimensionale Formen mit Kurven:
Zylinder	Kegel
Ein Zylinder hat den gleichen Querschnitt von einem Ende zum anderen. Zylinder haben zwei identische Enden eines Kreises oder eines Ovals. Obwohl ähnlich, sind Zylinder keine Prismen, da ein Prisma (per Definition) Parallelogramm, flache Seiten hat.,	Ein Kegel hat eine kreisförmige oder ovale Basis und einen Scheitelpunkt (oder Scheitelpunkt). Die Seite des Kegels verjüngt sich sanft zur Spitze. Ein Kegel ähnelt einer Pyramide, unterscheidet sich jedoch dadurch, dass ein Kegel eine einzelne gekrümmte Seite und eine kreisförmige Basis hat.
Kugel	Torus
Geformt wie ein ball oder eine Welt eine Kugel ist ein komplett rundes Objekt. Jeder Punkt auf der Oberfläche einer Kugel ist ein gleicher Abstand zum Mittelpunkt der Kugel.,	In der Form eines Rings, eines Reifens oder eines Donuts wird ein regelmäßiger Ringtorus gebildet, indem ein kleinerer Kreis um einen größeren Kreis gedreht wird. Es gibt auch komplexere form von tori.

Oberfläche

Unsere Seite zur Berechnung der Fläche erklärt, wie man die Fläche von zweidimensionalen Formen ausarbeitet und Sie müssen diese Grundlagen verstehen, um die Oberfläche dreidimensionaler Formen zu berechnen.

Bei dreidimensionalen Formen sprechen wir über die Oberfläche, um Verwirrung zu vermeiden.,

Sie können Ihr Wissen über die Fläche von zweidimensionalen Formen verwenden, um die Oberfläche einer dreidimensionalen Form zu berechnen, da jede Fläche oder Seite effektiv eine zweidimensionale Form ist.

Sie erarbeiten daher den Bereich jedes Gesichts und fügen sie dann zusammen.

Wie bei flachen Formen wird die Oberfläche eines Festkörpers in quadratischen Einheiten ausgedrückt: cm2,Zoll2, m2 usw. Weitere Details zu Maßeinheiten finden Sie auf unserer Seite Messsysteme.,

Beispiele für Oberflächenberechnungen

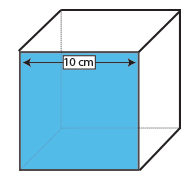
Cube

Die Oberfläche eines Würfels ist die Fläche einer Fläche (Länge x Breite) multipliziert mit 6, da alle sechs Flächen gleich sind.

Da die Fläche eines Würfels ein Quadrat ist, müssen Sie nur eine Messung durchführen – Länge und Breite eines Quadrats sind definitionsgemäß gleich.

Eine Fläche dieses Würfels ist daher 10 × 10 cm = 100cm2. Multiplizieren Sie mit 6, der Anzahl der Flächen auf einem Würfel, und wir stellen fest, dass die Oberfläche dieses Würfels 600cm2 beträgt.,

Andere reguläre Polyeder

In ähnlicher Weise kann die Oberfläche der anderen regulären Polyeder (platonische Feststoffe) ermittelt werden, indem die Fläche einer Seite ermittelt und dann die Antwort mit der Gesamtzahl der Seiten multipliziert wird – siehe das obige Grundpolyederdiagramm.

Wenn die Fläche eines Fünfecks, aus dem ein Dodekaeder besteht, 22cm2 beträgt, multiplizieren Sie dies mit der Gesamtzahl der Seiten (12), um die Antwort 264cm2 zu erhalten.,

Pyramide

Um die Oberfläche einer Standardpyramide mit vier gleichen dreieckigen Seiten und einer quadratischen Basis zu berechnen:

Erarbeiten Sie zuerst die Fläche der Basis (Quadrat) Länge × Breite.

Als nächstes den Bereich einer Seite (Dreieck) ausarbeiten. Messen Sie die Breite entlang der Basis und dann die Höhe des Dreiecks (auch als schräge Länge bezeichnet) vom Mittelpunkt der Basis bis zur Spitze.,

Sie können dann entweder Ihre Antwort durch 2 teilen, um die Oberfläche eines Dreiecks zu erhalten, und dann mit 4 multiplizieren, um die Oberfläche aller vier Seiten zu erhalten, oder einfach die Oberfläche eines Dreiecks mit 2 multiplizieren.

Addieren Sie schließlich die Fläche der Basis und der Seiten zusammen, um die Gesamtoberfläche der Pyramide zu ermitteln.

Um die Oberfläche anderer Pyramidentypen zu berechnen, addieren Sie die Fläche der Basis (als Grundfläche bezeichnet) und die Fläche der Seiten (Seitenfläche), möglicherweise müssen Sie die Seiten einzeln messen.,

Netzdiagramme

Ein geometrisches Netz ist ein zweidimensionales ‚Muster‘ für ein dreidimensionales Objekt. Netze können hilfreich sein, wenn Sie die Oberfläche eines dreidimensionalen Objekts ausarbeiten. Im Diagramm unten können Sie sehen, wie grundlegende Pyramiden aufgebaut sind, wenn die Pyramide „entfaltet“ ist, bleibt Ihnen das Netz.

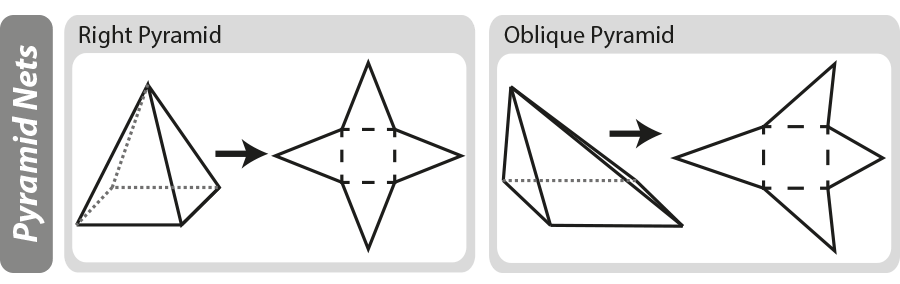
Weitere Informationen zu Netzdiagrammen finden Sie auf unserer Seite 3D-Formen und Netze.

Prisma

Um die Oberfläche eines Prismas zu berechnen:

Prismen haben zwei Enden die gleichen und flachen Parallelogrammseiten.,

Berechnen Sie die Fläche eines Endes und multiplizieren Sie mit 2.

Berechnen Sie für ein reguläres Prisma (bei dem alle Seiten gleich sind) die Fläche einer der Seiten und multiplizieren Sie sie mit der Gesamtzahl der Seiten.

Für unregelmäßige Prismen (mit verschiedenen Seiten) berechnen Sie die Fläche jeder Seite.

Addieren Sie Ihre beiden Antworten zusammen (Enden × Seiten), um die Gesamtoberfläche des Prismas zu ermitteln.,

Zylinder

Um die Oberfläche eines Zylinders zu berechnen, ist es sinnvoll, über die Bestandteile der Form nachzudenken. Stellen Sie sich eine Dose Zuckermais vor – sie hat eine Ober-und eine Unterseite, die beide Kreise sind. Wenn Sie die Seite entlang ihrer Länge schneiden und abgeflacht hätten, hätten Sie ein Rechteck. Sie müssen daher die Fläche von zwei Kreisen und einem Rechteck finden.

Erarbeiten Sie zuerst den Bereich eines der Kreise.

Die Fläche eines Kreises ist π(pi) × radius2.,

Bei einem Radius von 5 cm beträgt die Fläche eines der Kreise 3, 14 × 52 = 78, 5 cm2.

Multiplizieren Sie die Antwort mit 2, da es zwei Kreise 157cm2

Die Fläche der Seite des Zylinders ist der Umfang des Kreises × die Höhe des Zylinders.

Umfang ist gleich π x 2 × radius. In unserem Beispiel, 3.14 × 2 × 5 = 31.4

Messen Sie die Höhe des Zylinders – in diesem Beispiel beträgt die Höhe 10cm. Die Oberfläche der Seite ist 31,4 × 10 = 314cm2.,

Die Gesamtoberfläche kann durch Addieren der Fläche der Kreise und der Seite gefunden werden:

157 + 314 = 471cm2

Kegel

Bei der Berechnung der Oberfläche eines Kegels müssen Sie die Länge der ‚Schräge‘ verwenden.sowie der Radius der Basis.

es ist Jedoch relativ einfach zu berechnen:

Die Fläche des Kreises an der Basis des Kegels ist π(pi) × radius2.

In diesem Beispiel ist die Summe 3.14 × 52 = 3.14 × 25 = 78.,5cm2

Die Fläche der Seite, der abfallende Abschnitt, kann mit dieser Formel gefunden werden:

π (pi) × Radius × Länge der Neigung.

In unserem Beispiel beträgt die Summe 3,14 × 5 × 10 = 157 m2.

Fügen Sie schließlich die Grundfläche zum Seitenbereich hinzu, um die Gesamtoberfläche des Kegels zu erhalten.

78,5 + 157 = 235. 5cm2

Kugel

Die Oberfläche einer Kugel ist eine relativ einfache Erweiterung der Formel für die Fläche eines Kreises.

4 × π × radius2.,

Für eine Kugel ist es oft einfacher, den Durchmesser zu messen – den Abstand über die Kugel. Sie können dann den Radius finden, der die Hälfte des Durchmessers beträgt.

Der Durchmesser eines Standard-Tennisballs beträgt 2,6 Zoll. Der Radius beträgt daher 1,3 Zoll. Für die Formel benötigen wir den Radius im Quadrat. 1.3 × 1.3 = 1.69.

Die Oberfläche eines Tennisballs ist daher:

4 × 3.14 × 1.69 = 21.2264 Zoll2.,

Torus

Um die Oberfläche eines Torus zu berechnen, müssen Sie zwei Radiuswerte finden.

Der große oder große Radius (R) wird von der Lochmitte bis zur Ringmitte gemessen.

Der kleine oder kleinere Radius (r) wird von der Mitte des Rings bis zur Außenkante gemessen.

Das Diagramm zeigt zwei Ansichten eines Beispiel-Torus und wie man seine Radien (oder Radien) misst.,

Die Berechnung zur Ermittlung der Oberfläche erfolgt in zwei Teilen (einer für jeden Radius). Die Berechnung ist für jedes Teil gleich.

Die Formel lautet: surface area = (2nR) (2nr)

Um die Oberfläche des Beispiel-Torus zu ermitteln.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

Multipliziere die beiden, gemeinsam Antworten zu finden, die Gesamtfläche des Beispiel-torus.