tredimensionelle former: Polyhedroner, buede faste stoffer og overfladeareal

denne side undersøger egenskaberne for tredimensionelle eller ‘faste’ former.

en todimensionel form har længde og bredde. En tredimensionel solid form har også dybde. Tredimensionelle former har af deres natur en indvendig og en udvendig, adskilt af en overflade. Alle fysiske ting, ting du kan røre ved, er tredimensionelle.,

denne side dækker både lige-sidet faste stoffer kaldet polyhedroner, som er baseret på polygoner, og faste stoffer med kurver, såsom glober, cylindre og kegler.

polyeder

polyeder (eller polyhedra) er lige sidede faste former. Polyhedroner er baseret på polygoner, todimensionale planformer med lige linjer.

se vores side Egenskaber for polygoner for mere om at arbejde med polygoner.

polyeder er defineret som havende:

• lige kanter.
• flade sider kaldet ansigter.,
• hjørner, kaldet hjørner.

Polyhedroner defineres også ofte af antallet af kanter, ansigter og hjørner, de har, samt om deres ansigter har samme form og størrelse. Ligesom polygoner kan polyhedroner være regelmæssige (baseret på regelmæssige polygoner) eller uregelmæssige (baseret på uregelmæssige polygoner). Polyhedroner kan også være konkave eller konvekse.

en af de mest grundlæggende og velkendte polyhedroner er terningen. En terning er en almindelig polyhedron, der har seks firkantede ansigter, 12 kanter og otte hjørner.,

Regelmæssige Polyhedrons (Platoniske Legemer)

De fem regulære legemer er en særlig klasse af polyhedrons, hvis ansigter er identisk med hver enkelt ansigt bliver en regulær polygon. De platoniske faste stoffer er:

• Tetrahedron med fire ligesidede trekantflader.
• terning med seks firkantede ansigter.
• Octahedron med otte ligesidede trekantflader.
• Dodecahedron med tolv pentagon ansigter.
• Icosahedron med tyve ligesidede trekantflader.,

se diagrammet ovenfor for en illustration af hver af disse regelmæssige polyeder.

Hvad er et prisme?

et prisme er enhver polyhedron, der har to matchende ender og flade sider. Hvis du skærer et prisme overalt langs dens længde, parallelt med en ende, er dens tværsnit det samme-du ville ende med to prismer. Siderne af et prisme er parallelogrammer-firsidede former med to par sider med samme længde.

Antiprismer ligner almindelige prismer, deres ender matcher., Men siderne af anti-prismer består af trekanter og ikke parallelograms. Antiprismer kan blive meget komplekse.

Hvad er en pyramide?

en pyramide er en polyhedron med en polygonbase, der forbinder til en ape. (øverste punkt) med lige sider.

selvom vi har en tendens til at tænke på pyramider med en firkantet base, ligesom dem, som de gamle egyptere byggede, kan de faktisk have nogen polygonbase, regelmæssig eller uregelmæssig. Desuden kan en pyramide have en ape.i det direkte centrum af sin base, en højre pyramide, eller kan have Ape. off center, når det er en skrå pyramide.,

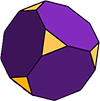
Mere Komplekse Polyhedrons

Der er mange flere typer af polyedre: symmetrisk og asymmetrisk, konkave og konvekse. arkimediske faste stoffer består for eksempel af mindst to forskellige regelmæssige polygoner.

den afkortede terning (som illustreret) er et arkimedisk faststof med 14 ansigter. 6 af ansigterne er regelmæssige ottekanter og de andre 8 er regelmæssige (ligesidede) trekanter. Formen har 36 kanter og 24 hjørner (hjørner).,

tredimensionelle former med kurver

faste former, der inkluderer en buet eller rund kant, er ikke polyhedroner. Polyhedroner kan kun have lige sider.

mange af objekterne omkring dig vil indeholde mindst nogle kurver. I geometri de mest almindelige buede faste stoffer er cylindre, kegler, kugler og tori (flertal for torus).,

Fælles Tre-Dimensionelle Figurer med Kurver:
Cylinder	Kegle
En cylinder har samme tværsnit fra den ene ende til den anden. Cylindre har to identiske ender af enten en cirkel eller en oval. Selvom lignende, cylindre er ikke prismer som et prisme har (per definition) parallelogram, flade sider.,	en kegle har en cirkulær eller oval base og en ape. (eller Verte.). Siden af keglen tilspidser jævnt til toppen. En kegle ligner en pyramide, men distinkt som en kegle har en enkelt buet side og en cirkulær base.
Sfære	Torus
Formet som en bold eller en globus, en kugle, der er en helt rund genstand. Hvert punkt på overfladen af en kugle er en lige stor afstand til midten af kuglen.,	formet som en ring, et dæk eller en doughnut, dannes en almindelig ring torus ved at dreje en mindre cirkel omkring en større cirkel. Der er også mere kompleks form for tori.

overfladeareal

vores side om beregning af område forklarer, hvordan man udarbejder området med todimensionelle former, og du er nødt til at forstå disse grundlæggende for at beregne overfladearealet for tredimensionelle former.

for tredimensionelle former taler vi om overfladeareal for at undgå forvirring.,

Du kan bruge din viden om området med todimensionelle former til at beregne overfladearealet af en tredimensionel form, da hvert ansigt eller side effektivt er en todimensionel form.

du træner derfor området for hvert ansigt og tilføjer dem derefter sammen.

som med flade former udtrykkes overfladearealet af et fast stof i firkantede enheder: cm2, inches2, m2 og så videre. Du kan finde flere detaljer om måleenheder på vores side systemer til måling.,

eksempler på Overfladearealberegninger

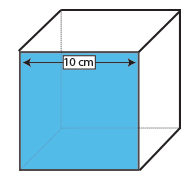
terning

overfladearealet af en terning er arealet af en flade (længde.bredde) multipliceret med 6, fordi alle seks flader er de samme.

da en kubes overflade er en firkant, behøver du kun at tage en måling – længden og bredden af en firkant er per definition den samme.

den ene side af denne terning er derfor 10 10 10 cm = 100cm2. Multiplicer med 6, antallet af ansigter på en terning, og vi finder ud af, at overfladearealet af denne terning er 600cm2.,

andre regelmæssige Polyhedroner

Tilsvarende kan overfladearealet af de andre regelmæssige polyhedroner (platoniske faste stoffer) udarbejdes ved at finde området på den ene side og derefter multiplicere svaret med det samlede antal sider – se det grundlæggende Polyhedrondiagram ovenfor.

hvis arealet af en femkant, der udgør en dodecahedron, er 22cm2, multipliceres dette med det samlede antal sider (12) for at give svaret 264cm2.,

pyramide

for at beregne overfladearealet af en standardpyramide med fire lige trekantede sider og en firkantet base:

træk først arealet af basen (firkantet) længde.bredde.

næste arbejde ud området på den ene side (trekant). Mål bredden langs bunden og derefter højden af trekanten (også kendt som skrå længde) fra det centrale punkt på basen til spidsen.,

Du kan derefter enten dele dit svar med 2 for at give dig overfladearealet af en trekant og derefter multiplicere med 4 for at give overfladearealet på alle fire sider, eller blot multiplicere overfladearealet af en trekant med 2.

Tilføj endelig arealet af basen og siderne sammen for at finde pyramidens samlede overfladeareal.

for at beregne overfladearealet for andre typer pyramider skal du tilføje basisarealet (kendt som basisareal) og arealet af siderne (lateralt område).,

netdiagrammer

et geometrisk net er et todimensionelt ‘mønster’ for et tredimensionelt objekt. Net kan være nyttige, når man udarbejder overfladearealet på et tredimensionelt objekt. I diagrammet nedenfor kan du se, hvordan grundlæggende pyramider er konstrueret, hvis pyramiden er ‘udfoldet’, står du tilbage med nettet.

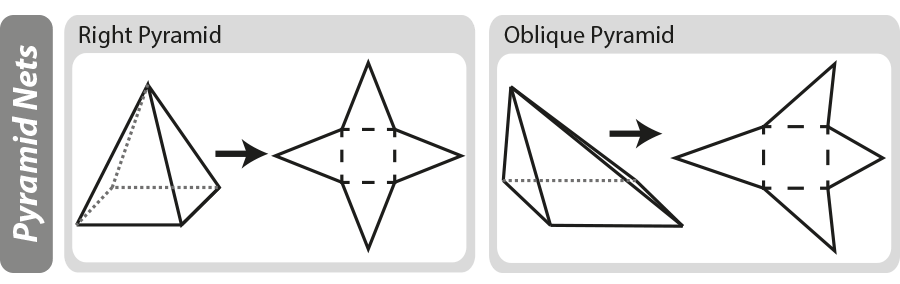
For mere om netto diagrammer Se vores side 3D former og Net.

Prisme

for At beregne overfladearealet af et prisme:

Prismer har to ender af det samme og fladskærms parallelogram sider.,

Beregn arealet af den ene ende og gang med 2.

for et regelmæssigt prisme (hvor alle sider er ens) beregnes arealet af en af siderne og multipliceres med det samlede antal sider.

for uregelmæssige prismer (med forskellige sider) beregnes arealet af hver side.

Tilføj dine to svar sammen (ender × sider) for at finde prismens samlede overfladeareal.,

Cylinder

for At beregne arealet af en cylinder, er det nyttigt at tænke på de dele af formen. Forestil dig en dåse sukkermajs-den har en top og en bund, som begge er cirkler. Hvis du skærer siden langs dens længde og fladder den, ville du have et rektangel. Du skal derfor finde arealet af to cirkler og et rektangel.

udfør først området for en af cirklerne.

arealet af en cirkel er π(pi) radi radius2.,

under forudsætning af en radius på 5 cm er arealet af en af cirklerne 3, 14.52 = 78, 5cm2.

Multiplicer svaret med 2, da der er to cirkler 157cm2

området på siden af cylinderen er cirklens omkreds × cylinderens højde. omkredsen er lig med radius 2 2 radius radius. I vores eksempel, 3.14 × 2 × 5 = 31.4

mål cylinderens højde – i dette eksempel er højden 10 cm. Overfladearealet af siden er 31,4 10 10 = 314cm2.,

Det samlede areal kan findes ved at tilføje det område af cirkler og side sammen:

157 + 314 = 471cm2

Kegle

ved beregningen af arealet af en kegle er du nødt til at bruge længden af den “skrå”, såvel som radius i bunden.

det er dog relativt ligetil at beregne:

området af cirklen ved bunden af keglen er π(pi). radius2.

i dette eksempel er summen 3.14 × 52 = 3.14 × 25 = 78.,5cm2

området på siden, det skrånende afsnit, kan findes ved hjælp af denne formel:

π(pi). radius. skrålængde.

i vores eksempel er summen 3.14 5 5.10 = 157cm2.

Tilføj til sidst basisarealet til sidearealet for at få keglens samlede overfladeareal.

78.5 + 157 = 235.5cm2

Sfære

overfladearealet af en kugle er en relativt simpel udvidelse af formlen for en cirkels areal.

4 radi radi radi radius2.,

for en kugle er det ofte lettere at måle diameteren – afstanden over kuglen. Du kan derefter finde radius, som er halvdelen af diameteren.

diameteren af en standard tennisbold er 2,6 tommer. Radius er derfor 1, 3 tommer. Til formlen har vi brug for radius kvadreret. 1.3 × 1.3 = 1.69.

overfladearealet af en tennisbold er derfor:

4 × 3.14 × 1.69 = 21.2264 inches2.,

Torus

for at beregne overfladearealet af en torus er du nødt til at finde to radius-værdier.

den store eller store radius (R) måles fra midten af hullet til midten af ringen.

den lille eller mindre radius (r) måles fra midten af ringen til yderkanten.

diagrammet viser to visninger af et eksempel torus og hvordan man måler dets radiuser (eller radier).,

beregningen for at finde overfladearealet er i to dele (en for hver radius). Beregningen er den samme for hver del.

formlen er: overfladeareal = (2nR)(2nr)

for at udarbejde overfladearealet af eksemplet torus.

(2 (R R R) = (2 × 3.14 × 20) = 125.6

(2 r r) = (2 × 3.14 × 4) = 25.12

Multiplicer de to svar sammen for at finde det samlede overfladeareal af eksemplet torus.