
En kort forklaring og bevis
Rational Rod Sætning (RRT) er et praktisk værktøj at have i din matematiske arsenal. Det giver og hurtig og beskidt test for rationaliteten af nogle udtryk. Og det hjælper med at finde rationelle rødder af polynomier.,
Her er hvordan og hvorfor det virker.,e53714″>
Hvordan
Antag at du har et polynomium af grad n, med heltal koefficienter:

Rational Rod Sætning hedder: Hvis en rational rod findes, derefter dets komponenter vil opdele den første og sidste koefficienter:

rational rod er udtrykt i laveste vilkår., Det betyder, at p og q deler ingen fælles faktorer. (Det vil være vigtigt senere.) Tælleren opdeler konstanten i slutningen af polynomet; demominatoren opdeler den førende koefficient.
Som et eksempel:
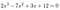
Vi skal kun se på de 2 og 12.,:
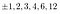
The factors of 2:
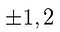
Thus, if a rational root does exist, it’s one of these:
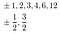
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
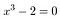
Furthermore:
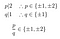
Not one of these candidates qualifies., Hop til:
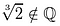
Hvorfor
Lad s gå tilbage til vores paradigme polynomium.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Formere sig alt af qⁿ:

Hver valgperiode på venstre p til fælles. Faktor det ud.,

Det ser meget værre end det behøver at være. Lad os erstatte alle de ting i parentes med en S. Vi er ligeglad med hvad der er derinde.
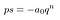
Det er meget lettere for øjnene.
Husk at p og q er heltal. De deler heller ingen fælles faktorer., Derfor kan p ikke opdele Q.. Det skal opdele a₀:
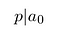
Således tælleren deler konstant sigt.
Nu, gå tilbage til vores paradigme polynomium:

Denne gang, bad den første periode til den rigtige side.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
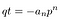
Again, q and p have no common factors. Therefore:
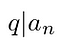
Thus proves the rational root theorem.