Bayes’ sætning finder mange anvendelser i sandsynlighedsteorien og statistikken. Der er en mikro chance for, at du aldrig har hørt om denne sætning i dit liv. Det viser sig, at denne sætning har fundet vej ind i maskinlæringsverdenen for at danne en af de højt dekorerede algoritmer. I denne artikel lærer vi alt om den Naive Bayes-algoritme sammen med dens variationer til forskellige formål i maskinlæring.
som du måske har gættet, kræver det os at se tingene fra et probabilistisk synspunkt., Ligesom i maskinlæring har vi attributter, responsvariabler og forudsigelser eller klassifikationer. Ved hjælp af denne algoritme vil vi beskæftige os med sandsynlighedsfordelingerne af variablerne i datasættet og forudsige sandsynligheden for responsvariablen, der tilhører en bestemt værdi, i betragtning af attributterne for en ny instans. Lad os starte med at gennemgå Bayes’ sætning.
Bayes’ sætning
Dette lader os undersøge sandsynligheden for en begivenhed baseret på forudgående kendskab til enhver begivenhed, der vedrører den tidligere begivenhed., Så for eksempel sandsynligheden for, at prisen på et hus er høj, kan vurderes bedre, hvis vi kender faciliteterne omkring det, sammenlignet med vurderingen foretaget uden kendskab til placeringen af huset. Bayes ‘ sætning gør netop det.

Ovenstående ligning giver de grundlæggende repræsentation af Bayes’ sætning., Her er A og B to begivenheder , og
P(A|B) : den betingede sandsynlighed for, at Begivenhed a forekommer, da B er forekommet. Dette er også kendt som den bageste Sandsynlighed.
p(a) og p(b) : Sandsynlighed for A og B uden hensyntagen til hinanden.
P(b|a) : den betingede sandsynlighed for , at Begivenhed B forekommer, da A er forekommet.
lad os nu se, hvordan dette passer godt til formålet med maskinlæring.,
Tag et simpelt maskinindlæringsproblem, hvor vi er nødt til at lære vores model fra et givet sæt attributter(i træningseksempler) og derefter danne en hypotese eller en relation til en responsvariabel. Så bruger vi denne relation til at forudsige et svar, givet attributter af en ny instans. Ved hjælp af Bayes’ sætning, Det er muligt at opbygge en elev, der forudsiger sandsynligheden for svaret variabel tilhører nogle klasse, givet et nyt sæt af attributter.
Overvej den forrige ligning igen. Antag nu, at A er responsvariablen, og B er inputattributten., Så ifølge ligningen har vi
P(A / B) : betinget sandsynlighed for responsvariabel, der tilhører en bestemt værdi, givet inputattributterne. Dette er også kendt som den bageste Sandsynlighed.
P(A) : den tidligere Sandsynlighed for responsvariablen.
P(b) : sandsynligheden for træningsdata eller beviset.
P(b|A) : Dette er kendt som sandsynligheden for træningsdataene.,
Derfor, ovenstående ligning kan skrives som
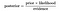
Lad os tage et problem, hvis antallet af attributter, der er lig med n, og svaret er en boolesk værdi, dvs det kan være i en af de to klasser. Attributterne er også kategoriske (2 kategorier for vores sag). For at træne klassifikatoren skal vi nu beregne P(B|A) for alle værdierne i instansen og responsområdet., Det betyder, at vi skal beregne 2 * (2^n -1), parametre til at lære denne model. Dette er klart urealistisk i de fleste praktiske læringsdomæner. For eksempel, hvis der er 30 boolske attributter, skal vi estimere mere end 3 milliarder parametre.
naiv Bayes-algoritme
kompleksiteten af den ovennævnte bayesiske klassifikator skal reduceres, for at den skal være praktisk. Den naive Bayes-algoritme gør det ved at antage en betinget uafhængighed over træningsdatasættet. Dette reducerer drastisk kompleksiteten af ovennævnte problem til kun 2n.,
en antagelse om betinget uafhængighed stater, der, givet stokastiske variable X, Y og Z, vi siger, at X er betinget uafhængige af Y givet Z, hvis og kun hvis den sandsynlighedsfordeling, der regulerer X er uafhængig af værdien af Y givet Z.
med andre ord, at X og Y er betinget uafhængige givet Z, hvis og kun hvis, givet viden om, at Z opstår, viden om X opstår, giver ingen oplysninger om sandsynligheden for at Y forekommende, og viden om Y opstår, giver ingen oplysninger om sandsynligheden for, at X sker.,
denne antagelse gør Bayes-algoritmen naiv.
i Betragtning af, n forskellige attributværdier, sandsynligheden for, nu kan skrives som
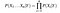
Her, er X repræsenterer de attributter eller egenskaber, og Y er responsvariabel. Nu, P (|/Y) bliver lig med produkterne af, sandsynlighedsfordeling af hver attribut given givet Y.,
maksimering af en Posteriori
hvad vi er interesseret i, er at finde den bageste Sandsynlighed eller P(Y/.). For flere værdier af Y skal vi nu beregne dette udtryk for hver af dem.
givet en ny instans XNE., er vi nødt til at beregne sandsynligheden for, at Y vil påtage sig en given værdi, givet de observerede attributværdier for .ne. og givet fordelingerne P(Y) og p (. / y) estimeret ud fra træningsdataene.
så hvordan vil vi forudsige klassen af responsvariablen, baseret på de forskellige værdier, vi opnår for P(Y/.)., Vi tager simpelthen det mest sandsynlige eller maksimale af disse værdier. Derfor er denne procedure også kendt som at maksimere a posteriori.
maksimere sandsynligheden
Hvis vi antager, at responsvariablen er ensartet fordelt, er det lige så sandsynligt, at det får noget svar, så kan vi yderligere forenkle algoritmen. Med denne antagelse bliver priori eller P (Y) en konstant værdi, som er 1/kategorier af svaret.
da priori og beviser nu er uafhængige af responsvariablen, kan disse fjernes fra ligningen., Derfor reduceres maksimeringen af posteriori til at maksimere sandsynlighedsproblemet.
Funktionsfordeling
som det ses ovenfor, er vi nødt til at estimere fordelingen af responsvariablen fra træningssæt eller antage ensartet fordeling. Tilsvarende, at estimere parametrene for en funktion distribution, man skal antage en fordeling eller generere ikke-parametriske modeller for funktionerne fra træningssættet. Sådanne antagelser er kendt som begivenhedsmodeller. Variationerne i disse antagelser genererer forskellige algoritmer til forskellige formål., For kontinuerlige distributioner er de gaussiske naive Bayes den valgte algoritme. For diskrete funktioner, multinomial og Bernoulli distributioner som populære. Detaljeret diskussion af disse variationer er uden for denne artikels anvendelsesområde.Naive Bayes-klassifikatorer fungerer rigtig godt i komplekse situationer på trods af de forenklede antagelser og naivitet. Fordelen ved disse klassifikatorer er, at de kræver et lille antal træningsdata til estimering af de parametre, der er nødvendige for klassificering. Dette er den valgte algoritme til tekstkategorisering., Dette er den grundlæggende id.bag naive Bayes classifiers, at du skal begynde at eksperimentere med algoritmen.