Calculate Log & Antilog Online (Dansk)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

hvor,

• b = base,
• y = nummer,
• = = logværdi.

beregning af Antilog:

y = 10.

hvor,

• = = tal,
• y = antilog værdi.

Logaritmer og Anti-Logaritmer: Hvordan Det Fungerer, og Dens Betydning

– Guide Forfattet af Corin B. Arenaer, udgivet oktober 1, 2019

Hvis du har nogensinde undret dig over, hvordan eksperter afgøre, store afstande, jordskælvs intensitet, og den globale økonomiske vækst priser, så er du kommet til det rette sted.

beregning af meget store summer kan være langsom og forvirrende., Men ved hjælp af logaritmer (log) og antilogaritmer (antilog) kan beregninger gøres enklere.

læs videre for at lære mere om log og antilog, hvordan de fungerer, og hvorfor disse er relevante matematiske begreber.

Hvad er logaritme?

en logaritme er den effekt, som et tal (benævnt basen) skal multipliceres til sig selv for at opnå et givet tal. I enklere termer løser logaritmen problemet:

hvor mange gange multiplicerer vi b for at få et andet nummer y?,

logaritme tæller antallet af gange den samme faktor skal ganges for at nå frem til et givet tal.

hvem kom op med det?

Log blev opfundet i det 16.århundrede som et beregningsværktøj af skotsk matematiker, fysiker og astronom, John Napier. Han skrev bogen Mirifici Logarithmorum Canonis Descriptio med tabeller og tal diskuterer naturlige logaritmer, fastsættelse af grundlaget for dets grundlæggende koncept.

Napier opfandt udtrykket logaritme fra det græske ord logoer som betyder ‘ratio eller andel,’ og arithmos som betyder ‘nummer.,’Når det kombineres, betyder det bogstaveligt’ ratio nummer.’

2 typer logaritmer

den naturlige logaritme af et tal er dens log til bunden af konstanten e, hvor e er omtrent lig med 2.718281828459. Ligningen er skrevet som loge (.).

hvis en logaritme ikke angiver en base, som dette eksempel: log(1000), er det kendt som en almindelig logaritme, der bruger basen 10.

log(1000), Det er kendt som en fælles logaritme, der bruger basen 10.

hvordan bruges Log?,

Når du begynder at beregne tal med millioner, milliarder og billioner, kan det blive ret beskattende. Uanset om det drejer sig om at tælle mange penge, væksten af befolkninger eller dækker store afstande, kan log arbejde for dig. Det kan forenkle store summer, der involverer lange og forvirrende ligninger, hvilket gør dem lettere at forstå.

Her er standardligningen for log:
logb(log) = y

hvor,

• tallet multipliceret til sig selv (B) er basen.
• antallet af gange det multipliceres (y) er logaritmen.,
• det opnåede tal ()) er skrevet i parentes.

for at forstå, hvordan konceptet fungerer, her er et eksempel med et mindre antal:
spørgsmål: Hvor mange 2 ‘ er multiplicerer vi for at få 32?
b = 2, Log = 32

log2(32) = y
svar: 2.2. 2. 2 = 2=32

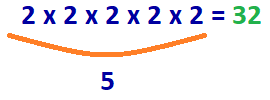
5 nummer 2s skal multipliceres for at opnå tallet 32.
svar: log2(32) = 5

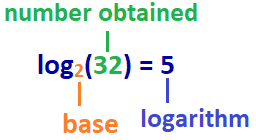
Derfor, i dette eksempel: Den naturlige logaritme af 32 med base 2 er 5, eller log base 2 af 32 5.,

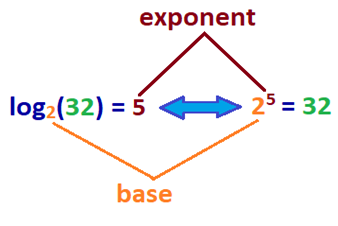
desuden er log den inverse funktion af eksponentiering, hvor den matematiske operation er skrevet som bn. b er den base, der multipliceres i henhold til kraften i n, hvilket er antallet af gange det multipliceres til sig selv.

Hvad betyder dette? Loggen af et tal er den eksponent, som base b Ganges for at opnå et givet tal. For at give dig en bedre id.henvises til prøvelogens ligning, der er indstillet sammen med dens eksponentielle ligning nedenfor.,

log ind	eksponent
log 2(32) = 5	25 = 32

lad os Nu prøve det med et stort antal.spørgsmål: Hvor mange 10 ‘ er multiplicerer vi for at få 150.000.000.000?
b = 10, x = 150,000,000,000

logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.,1760912590557

dette løses ved at bruge logfunktionen i en videnskabelig lommeregner. Eller brug lommeregneren på denne side for at få svaret.

Hvordan er antilogaritme relateret til Log?

et lognummer kan derefter returneres til dets oprindelige nummer. Dette kan gøres ved hjælp af antilogaritme (antilog). Således er antilog den inverse funktion af log. På samme måde fungerer antilog til at eksponentiere en forenklet logværdi.,

for At beregne antilog af en række y, skal du øge den naturlige logaritme base b (regel 10, nogle gange er den konstante e) til den magt, der vil generere antallet y.

Her er ligningen for antilog ved hjælp af base 10:
10x = y
, Hvor x er eksponent og y er antilog værdi. hvis vi for eksempel tager denne ligning, log (5)=., vil dens antilog være 10 = = 5.

• Log: log(5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

lad os Nu prøve det med et større antal.,

Hvis vi tager log(150,000,000,000)=., vil dens antilog være 10. = 150,000,000,000.

• Log: log10(150,000,000,000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150,000,000,000

Betydning og den Virkelige Verden

Forud for opfindelsen af regnemaskiner, logaritmer blev brugt til at forenkle beregninger i forskellige områder af viden, såsom navigation, landmåling, i astronomi, og senere ingeniør.

Forestil dig at sejle midt i intetsteds i det 16.århundrede., Navigatorer dengang påberåbt sig placeringen af stjerner og en sekstant mekanisme til at lokalisere deres nøjagtige placering. Uden moderne teknologi til at hjælpe dig med at beregne store afstande, kan du bruge log til at forenkle dine beregninger. Nøjagtighed er vigtig, eller du risikerer flere dage til søs med beskedne forsyninger. Færre ligninger betyder mindre plads til fejl.

hvad med andre praktiske anvendelser? Levende Videnskab stater logaritmer relatere geometriske progressioner til aritmetiske progressioner., Hvis du nogensinde har bemærket gentagne former og mønstre i naturen, arkitektur og kunst, besidder disse formationer deres egne tilsvarende logaritmiske værdier.

i dag påvirker viden om, hvordan disse mønstre fungerer, den måde, menneskeheden konstruerer og designer huse, bygninger og bylandskaber.

logaritmer bruges også til at udtrykke omfanget og intensiteten af visse skalaer., Bortset fra lang afstand, og høje hastigheder, er det foranstaltninger, der er andre ting, såsom:

• Sound intensity
• Lyd-frekvens
• Kraft af windstorms
• Styrken af jordskælv
• Ætsende niveau af fedtsyrer
• Hårdhed af mineraler
• Lysstyrke af stjerner

Lad os tage decibel som et eksempel. For at gøre højttalere højere med 10 decibel, skal den leveres med 10 gange strømmen. Når du øger den til + 20 dB, har den brug for 100 gange strømmen, og med +30 dB har den brug for 1.000 strømmen.

desuden Udvikler lydintensiteten aritmetisk., Det ændrer sig også proportionalt med logaritmen af en lydbølge, der skrider frem geometrisk.

nedenfor er en tabel fra Live Science, der viser forskellige logaritmiske skalaer med deres tilsvarende lineære skalaer.

I Måling af Priser og Rækker

Ifølge for at Kalid Azad, matematik pædagog bag BetterExplained.com, logaritmer er, hvordan vi regne ud, hvor hurtigt noget er stigende.

almindelige logaritmer beskriver dybest set tal med hensyn til deres beføjelser på 10. Når det kommer til rente, logaritmen er væksten i en investering.,

Ved fastsættelsen af BNP-vækstraten i et land gennemgår analytikere BNP i de efterfølgende år. De tager BNP i det foregående år, og BNP det følgende år, derefter beregne logaritmen at finde den anslåede vækstrate.

søgemaskiner bruger linkgrafen til at hjælpe med at score vigtigheden, troværdighed & autoritet af dokumenter på tværs af internettet. Googles PageRank var en stor udvikling i søgning, som boostet søgning relevans og hjalp Google søgning marketshare.,

ifølge A .ad, i en skala fra 1 til 10, er en destinationsside med en PageRank på 2 10 gange mere populær end en side med en PageRank på 1. Hvis et siteebsted har en PageRank på 5, og et konkurrent siteebsted har en PageRank på 9, har det en forskel på 4 størrelsesordener.

en størrelsesorden betyder omtrent en 10 difference forskel, eller en placering er 1 ciffer større sammenlignet med den anden. I dette tilfælde er et Pagebsted med en PageRank 9 100.000.000 mere populært end et .ebsted med PageRank 1.,

bundlinjen

Log og antilog er betydelige computermetoder, der giver os mulighed for at forenkle store summer. Forenkling forkorter beregningsprocessen og gør beregningerne lettere at forstå. Dette hjælper med at reducere plads til fejl.

Desuden giver brug af log målbare skalaer til måling af naturfænomen, som jordskælvintensitet, vindstormens kraft og stjernernes lysstyrke. Med hensyn til finansiering giver logaritmer os mulighed for at fastlægge renter og økonomiske vækstrater.

det bruges praktisk talt i mange felter., Store værdier, der afhænger af målingens nøjagtighed, drager fordel af at bruge logaritmiske beregninger.

om forfatteren

Corin er en ivrig forsker og forfatter af økonomiske emner—studerer økonomiske tendenser, hvordan de påvirker befolkningen, samt hvordan man hjælper forbrugerne med at træffe klogere økonomiske beslutninger. Hendes øvrige artikler kan læses på Inquirer.net og Manileno.com. Hun har en Master ‘ s degree i Kreativ Skrivning fra University of the Philippines, en af de førende akademiske institutioner i verden, og en Bachelor i Kommunikation Arts fra Miriam College.