at Finde den kvadratiske funktioner for givet parabler – Kvadratiske Funktioner

Find den Kvadratiske Funktioner for Givet Parabler

Der er så mange forskellige typer af problemer, du kan blive bedt om med hensyn til kvadratiske ligninger. I denne artikel vil fokus blive placeret på, hvordan vi kan udvikle en kvadratisk ligning fra en kvadratisk graf ved hjælp af et par forskellige metoder., Men, før vi kommer ind i disse typer af problemer, tage et øjeblik til at lege med kvadratiske udtryk på denne vidunderlige online grafregner her. Jo mere behagelig du er med kvadratiske grafer og udtryk, jo lettere vil dette emne være!

lad os nu løse problemer med denne viden, nemlig hvordan man finder ligningen af en parabola!

Sådan finder du en kvadratisk ligning fra en graf:

for at finde en kvadratisk ligning fra en graf er der to enkle metoder, man kan anvende: ved hjælp af 2 point eller ved hjælp af 3 point.,1) Find kvadratisk ligning fra 2 point

for at finde en kvadratisk ligning fra en graf, der kun bruger 2 point, skal et af disse punkter være Verte .et. Med Verte .et og et andet punkt kan vi sub disse koordinater ind i det, der kaldes “Verte .formen” og derefter løse for vores ligning., Vertex formlen er som følger, hvor (d,f) er toppunkt punkt og (x,y) er det andet punkt:

(y±d)=a(x±f)2(y \pm d) = a(x \pm f)^{2}(y±d)=a(x±f)2

Vertex form kan også være skrevet i sin mere “korrekt” form, som:

y=a(x±f)2∓dy = a(x \pm f)^{2} \mp dy=a(x±f)2∓d

ved Hjælp af denne formel, alt vi behøver at gøre, er at sub i issen, og det andet punkt, løse for en, og derefter omskrive vores endelige ligning., Den bedste måde at blive fortrolig med at bruge denne formular er at gøre et eksempel problem med det.

eksempel:

Bestem ligningen for parabolen vist på billedet nedenfor.

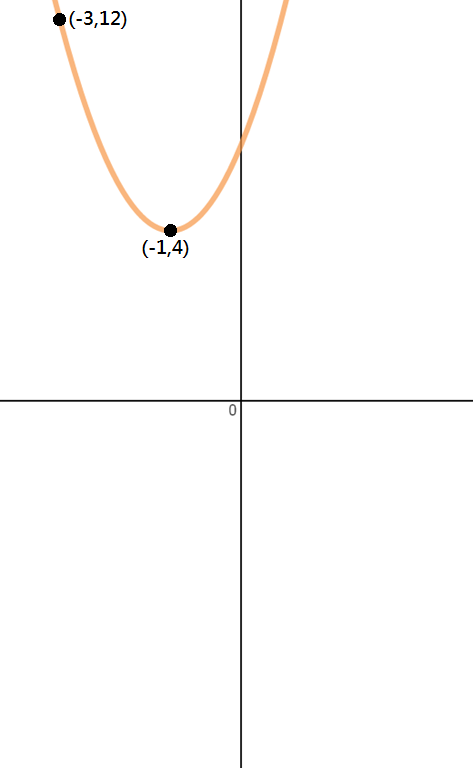
Trin 1: Identificere Punkter

Da vi kun fået to point i dette problem, isse og et andet punkt, vi skal bruge vertex form for at løse dette spørgsmål.,

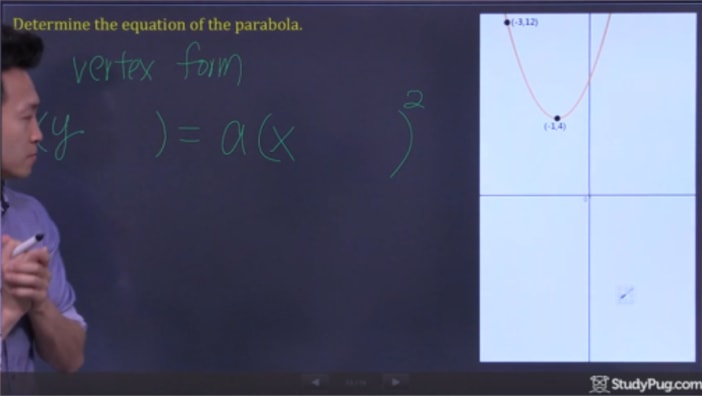
Trin 2: Sub-Point Til Vertex Form og Løse for “et”

Nu, vi alle skal gøre, er sub i vores to punkter i vertex formel og løse for “en” til at få alle oplysninger om at skrive vores afsluttende andengradsligning.,4)=en(-3+1)2(12 – 4) = en(-3 + 1)^{2}(12-4)=en(-3+1)2

8=a(-2)28 = a(-2)^{2}8=a(-2)28=4a8 = 4a8=4aa=2a = 2a=2

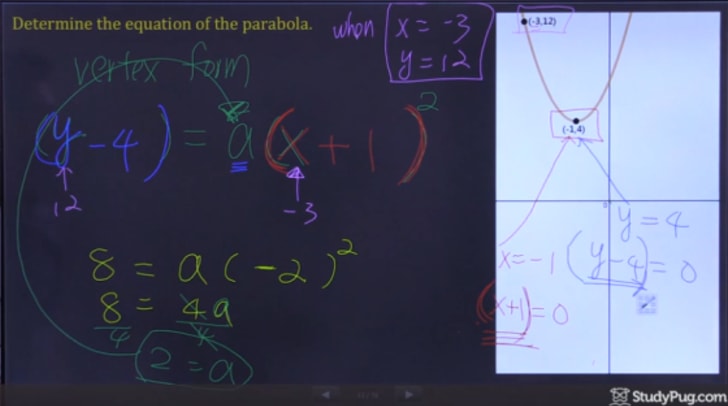
Trin 3: Skriv Ud andengradsligning

Når du har løst til “a”, vi har nu alle oplysninger, som vi er nødt til at skrive vores endelige svar.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

Og derefter i korrekt vertex form af en parabel, vores endelige svar er:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

Der fuldender lektion på vertex form, og hvordan til at finde en andengradsligning fra 2 point!, Hvis du vil opdatere din hukommelse om de relaterede emner som, hvordan man løser kvadratiske udtryk i Verte .form, hvordan man konverterer en almindelig kvadratisk ligning fra standardformular til Verte .form ved at udfylde firkanten, og hvordan man bruger Verte .formel, skal du sørge for at tjekke vores lektioner.2) Find kvadratisk ligning fra 3 point

i nogle tilfælde vil vi ikke være så heldige at få punktet på Verte .et. Hvis det er tilfældet, kan vi ikke længere finde det kvadratiske udtryk ved hjælp af kun to punkter og skal gøre noget lidt anderledes., I tilfælde af at vi får information om par-aflytninger af en parabola, såvel som et andet punkt, kan vi finde den kvadratiske ligning ved hjælp af en ligning, der kaldes “factored form”. Den generelle ligning for den, der er indregnet form formlen er som følger, med b, og c er den x-koordinat-værdier fra x-aflytninger:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

ved Hjælp af denne formel, alt vi behøver at gøre, er at sub i x-koordinater af x-aflytninger, et andet punkt, og derefter løse for en, så vi kan skrive vores endelige svar., Igen er den bedste måde at blive fortrolig med denne form for kvadratiske ligninger at gøre et eksempel problem.

Eksempel:

Bestem ligningen for parablen, der er vist på billedet nedenfor:

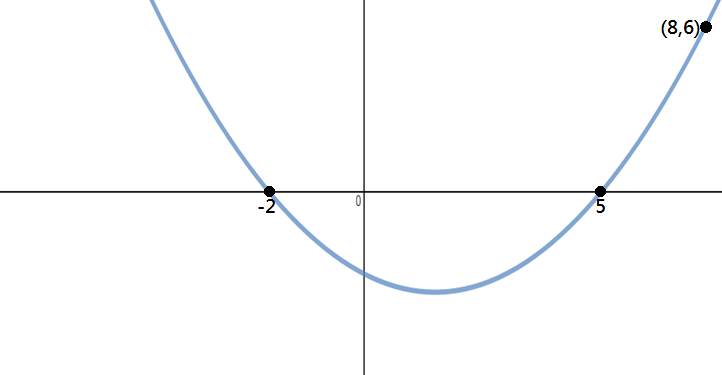
Trin 1: Identificere Punkter

Da vi får tre point i dette problem, x-aflytninger og et andet punkt, vi kan bruge indregnes form for at løse dette spørgsmål.,

fra grafen kan vi se, at intercep-aflytningerne er -2 og 5, og punktet på parabolen er (8,6).

Trin 2: Sub-Point Til Vertex Form og Løse for “et”

Nu, vi alle skal gøre, er sub i vores værdier i indregnes form formel og løse for “en” til at få alle oplysninger om at skrive vores afsluttende andengradsligning.,(x – 5)y=(x+2)(x−5)

Næste, kan vi bruge det punkt på en parabel (8,6) til at løse for “a”:

6=en(8+2)(8-5)6 = en(8 + 2)(8 – 5)6=a(8+2)(8-5)6=a(10)(3)6 = a(10)(3)6=a(10)(3)6=30a6 = 30a6=30aa=15a = \frac{1}{5}a=51

Trin 3: Skriv Ud andengradsligning

Når du har løst til “a”, vi har nu alle oplysninger, som vi er nødt til at skrive vores endelige svar.,

y=15 (++2)(5−5)y = \frac{1}{5} (!+2)(5 – 5)y=51 (! + 2) (!−5)

og det er alt der er til det! Det er de to vigtigste metoder til at finde en kvadratisk funktion fra en given parabola. For yderligere undersøgelse i Kvadratisk funktioner og deres grafer, tjek disse nyttige videoer beskæftiger sig med discriminant, graftegning kvadratisk ulighed, og conic sektioner.