1913 Bohr model for hydrogenatomet blev erstattet af Schrodingerʹs bølge mekanisk model i 1926. Men Bohrʹs-modellen er stadig rentabelt lært i dag på grund af dens konceptuelle og matematiske enkelhed, og fordi der blev indført en række centrale kvantemekaniske ideer som kvantemekanikken, kvantisering af de observerbare egenskaber, quantum spring og stationære tilstand.,
Bohr beregnet manifolden af tilladte elektronenergier ved at afbalancere de mekaniske kræfter (centripetal og elektron‐kerne) på en elektron, der udfører en cirkulær bane med radius R om kernen og derefter arbitrært kvantiserer dens vinkelmoment. Endelig fiat han erklærede, at elektronen var i en ikke‐udstrålende stationær tilstand, fordi en kredsende (fremskynde) afgift udstråler energi og vil kollapse i modsat ladning kerne.,
I 1924 de Broglie postulerede, bølge‐partikel dualitet for elektroner og andre massive partikler, hvilket giver mulighed for at fjerne nogle af de arbitariness fra Bohrʹs model. For eksempel er en elektron, der besidder bølgeegenskaber, udsat for konstruktiv og destruktiv interferens. Som det vil blive vist, fører dette naturligt til Kvantisering af elektronmomentum og kinetisk energi, og følgelig et manifold af tilladte energitilstande for elektronen i forhold til kernen., De Broglie-Bohr-modellen af hydrogenatomet, der præsenteres her, behandler elektronen som en partikel på en ring med bølgelignende egenskaber.
\
de Broglies hypotese om, at sagen har bølgelignende egenskaber.
\
konsekvensen af de Broglie hypothesiss hypotese; et integreret antal bølgelængder skal passe inden for kredsløbets omkreds. Dette introducerer quantumuantum nummer, som kan have værdier 1,2,3,… N = 4 elektron tilstand er vist nedenfor.,
\
Substitution af den første ligning i den anden ligning viser, at momentum er kvantiseret.
\
hvis momentum er kvantiseret, så er kinetisk energi.
\
hvilket betyder, at den samlede energi er kvantiseret. Det andet udtryk er den elektron‐proton elektrostatiske potentielle energi.
den kvantemekaniske fortolkning af dissebobohr-orbits is er, at de er stationære tilstande. På trods af at vi bruger udtrykket kinetisk energi, hvilket indebærer elektronbevægelse, er der ingen bevægelse., Elektronen optager kredsløbet som en partikelbølge, den kredser ikke om kernen. Hvis det kredsede i klassisk forstand, ville det udstråle energi og hurtigt kollapse i kernen. Det er klart, at stoffets stabilitet kræver den kvantemekaniske version af kinetisk energi.
jordtilstandsenergien og kredsløbsradius for elektronen i hydrogenatomet findes ved at plotte energien som en funktion af den orbitale radius. Jordtilstanden er minimumet i den samlede energikurve., Naturligvis calculus kan bruges til at opnå de samme oplysninger ved at minimere energi med hensyn til orbit radius. Den grafiske metode har imidlertid dyden til at belyse spørgsmålet om atomstabilitet.grundlæggende konstanter: elektronladning, elektronmasse, Plancks konstant, vakuumpermitivitet.
factuantum antal og konvertering fakta mellem målere og picometre og Joule og Attojoule.
\
\
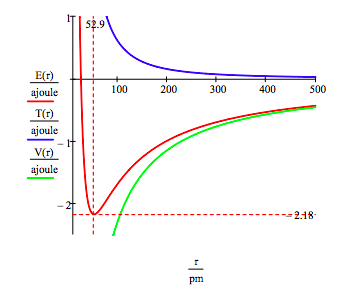
dette tal viser, at atomstabilitet indebærer en balance mellem potentiel og kinetisk energi., Elektronen trækkes mod kernen af den attraktive potentielle energiinteraktion (~-1/R), men forhindres i at kollapse i kernen af den ekstremt store kinetiske energi (~1/R2), der er forbundet med små baner.
som vist nedenfor kan den grafiske tilgang også bruges til at finde de elektroniske ophidsede tilstande.
\
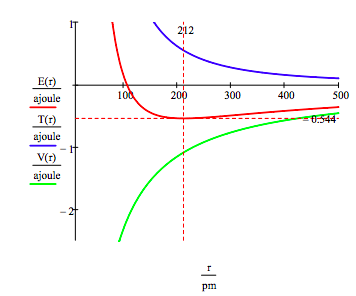
som tidligere nævnt kan manifolden af tilladte elektronenergier også opnås ved at minimere energien med hensyn til baneradius. Denne procedure giver,