Forholdet mellem Tryk og Volumen: boyles Lov
Som det pres på gas stiger, mængden af gas falder, fordi den gas partikler er tvunget tættere sammen. Omvendt, når trykket på en gas falder, øges gasvolumenet, fordi gaspartiklerne nu kan bevæge sig længere fra hinanden., Vejrballoner bliver større, når de stiger gennem atmosfæren til områder med lavere tryk, fordi volumenet af gassen er steget; det vil sige, at den atmosfæriske gas udøver mindre tryk på ballonens overflade, så den indvendige gas udvides, indtil det indre og ydre tryk er ens.
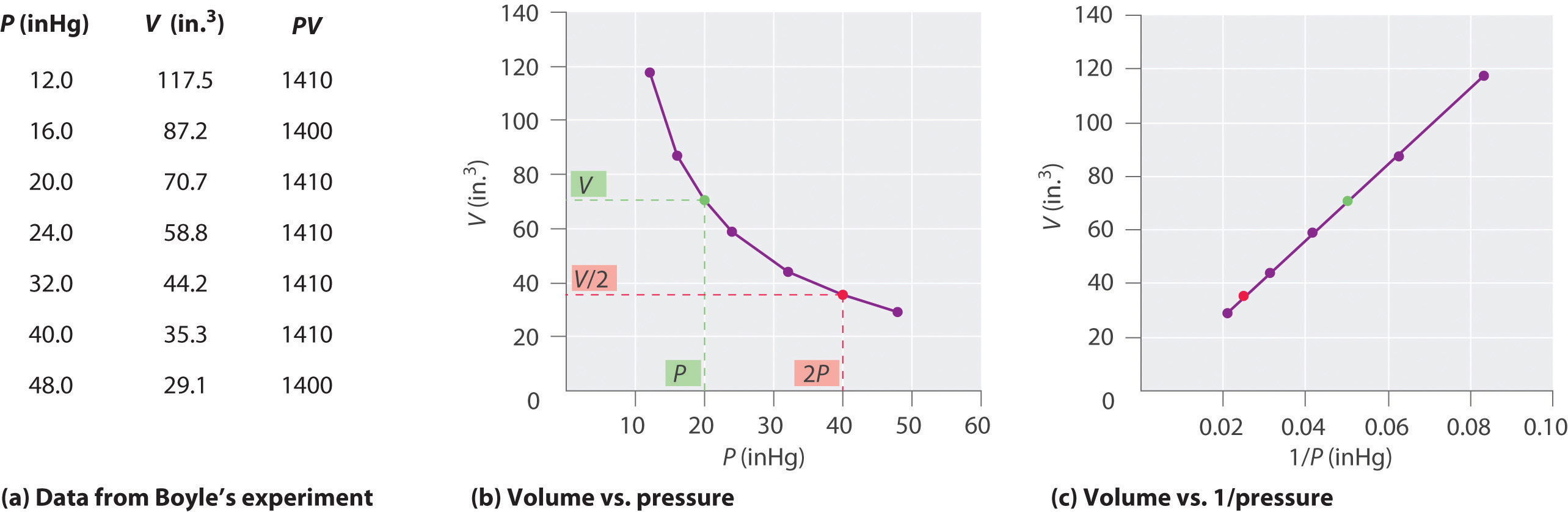
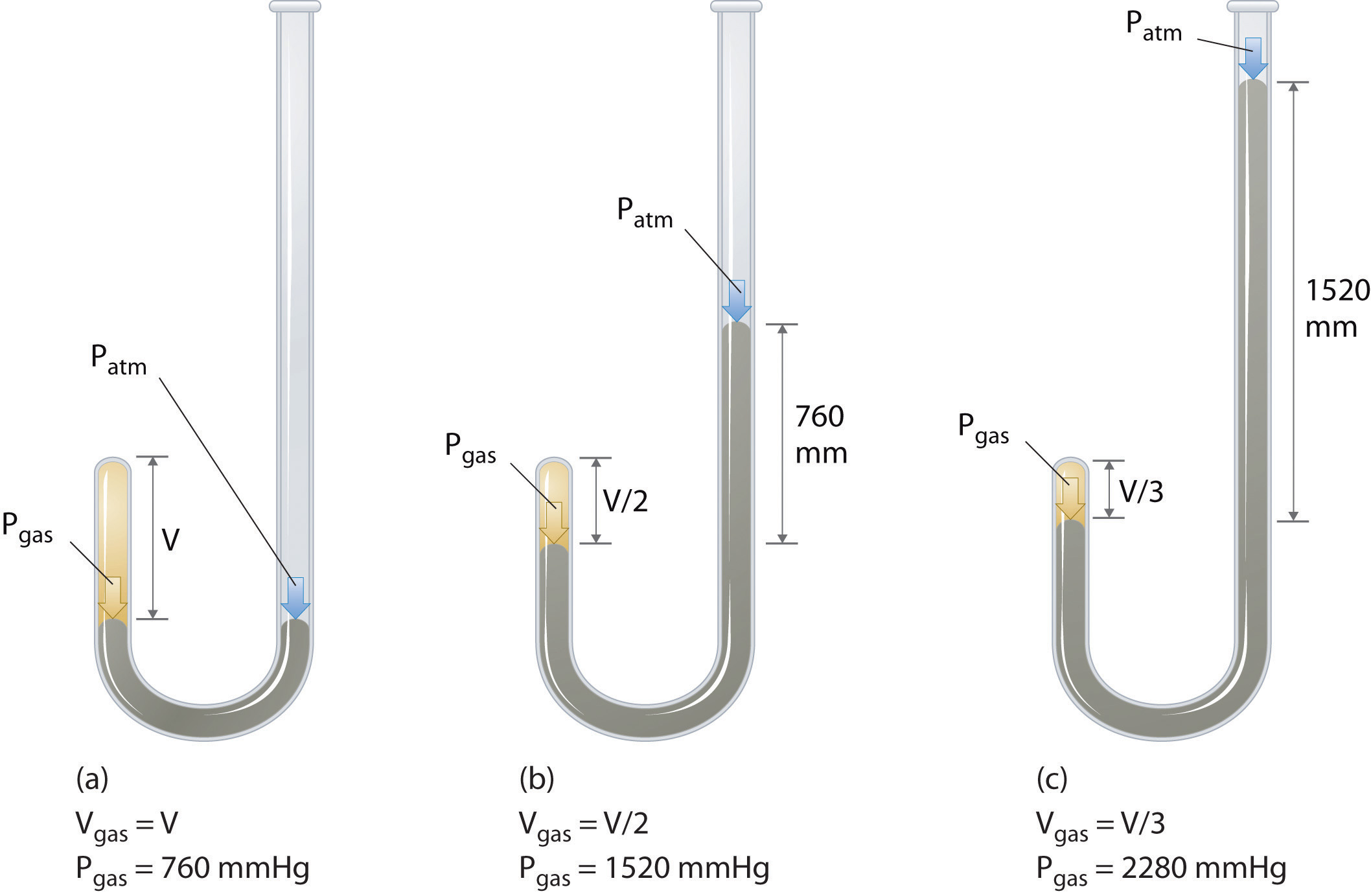
den irske kemiker Robert Boyle (1627-1691) udførte nogle af de tidligste eksperimenter, der bestemte det kvantitative forhold mellem trykket og volumenet af en gas. Boyle brugte et J-formet rør delvist fyldt med kviksølv, som vist i figur \(\Pageinde. {1}\)., I disse eksperimenter er en lille mængde af en gas eller luft fanget over kviksølvkolonnen, og dens volumen måles ved atmosfærisk tryk og konstant temperatur. Mere kviksølv hældes derefter i den åbne arm for at øge trykket på gasprøven. Trykket på gassen er atmosfærisk tryk plus forskellen i højderne af kviksølvsøjlerne, og det resulterende volumen måles. Denne proces gentages, indtil enten der ikke er mere plads i den åbne arm, eller volumenet af gassen er for lille til at måles nøjagtigt., Data som dem fra en af Boyles egne eksperimenter kan afbildes på flere måder (figur \(\Pageinde. {2}\)). Et simpelt plot af \(v\) versus \(P\) giver en kurve kaldet en hyperbola og afslører et omvendt forhold mellem tryk og volumen: når trykket fordobles, falder volumenet med en faktor på to. Denne relation mellem to mængder, der er beskrevet som følger:
\
opdeling af begge sider med \(p\) giver en ligning, der illustrerer det omvendte forhold mellem \(p\) og \(V\):
\
eller
\
hvor symbol-symbolet læses “er proportional med.”Et plot af V versus 1/P er således en lige linje, hvis hældning er lig med konstanten i ligning 6.2.1 og ligning 6.2.3. At dele begge sider af ligning 6.2.1 med V i stedet for P giver et lignende forhold mellem P og 1 / V., Den numeriske værdi af konstanten afhænger af mængden af gas, der anvendes i eksperimentet, og af den temperatur, ved hvilken eksperimenterne udføres. Dette forhold mellem tryk og volumen er kendt som Boyle ‘ s lov, efter sin opdager, og kan specificeres som følger: Ved konstant temperatur, mængden af et fast beløb af en gas er omvendt proportional med dens tryk.