Trojrozměrné Tvary: Polyhedrons, Zakřivené Objemy a Plochy

Tato stránka zkoumá vlastnosti tří-dimenzionální nebo ‚pevné‘ tvary.

dvourozměrný tvar má délku a šířku. Trojrozměrný pevný tvar má také hloubku. Trojrozměrné tvary mají svou povahou vnitřní a vnější, oddělené povrchem. Všechny fyzické předměty, věci, kterých se můžete dotknout, jsou trojrozměrné.,

tato stránka pokrývá jak přímé pevné látky zvané polyhedrony, které jsou založeny na polygonech, tak pevné látky s křivkami, jako jsou glóby, válce a kužely.

mnohostěny

mnohostěny (nebo mnohostěny) jsou rovné pevné tvary. Polyhedrony jsou založeny na polygonech, dvourozměrných rovinných tvarech s přímkami.

podívejte se na naše stránky vlastnosti polygonů pro více informací o práci s polygony.

polyhedrony jsou definovány jako:

• rovné hrany.
• ploché strany zvané tváře.,
• rohy, nazývané vrcholy.

polyhedrony jsou také často definovány počtem hran, ploch a vrcholů, které mají, a také tím, zda jejich tváře mají stejný tvar a velikost. Stejně jako polygony mohou být mnohostěny pravidelné (založené na pravidelných polygonech) nebo nepravidelné (založené na nepravidelných polygonech). Polyhedrony mohou být také konkávní nebo konvexní.

jedním z nejzákladnějších a nejznámějších mnohostěn je kostka. Kostka je pravidelný mnohostěn, který má šest čtvercových ploch, 12 okrajů a osm vrcholů.,

Pravidelné Polyhedrons (Platonické Pevné látky)

pět pravidelných těles jsou speciální třídy polyhedrons, jejichž tváře jsou totožné s každým tváří, že pravidelný mnohoúhelník. Platonické pevné látky jsou:

• čtyřstěn se čtyřmi rovnostrannými trojúhelníkovými plochami.
• kostka se šesti čtvercovými plochami.
• oktahedron s osmi rovnostrannými trojúhelníkovými plochami.
• Dodecahedron s dvanácti tvářemi Pentagonu.
• Icosahedron s dvaceti rovnostrannými trojúhelníkovými plochami.,

viz obrázek výše pro ilustraci každého z těchto pravidelných mnohostěn.

co je hranol?

hranol je jakýkoli polyhedron, který má dva odpovídající konce a ploché strany. Pokud vyříznete hranol kdekoli podél jeho délky, rovnoběžně s koncem, jeho průřez je stejný-skončili byste se dvěma hranoly. Strany hranolu jsou rovnoběžníky-čtyřstranné tvary se dvěma páry stran se stejnou délkou.

Antiprismy jsou podobné běžným hranolům, jejich konce odpovídají., Nicméně strany Anti-hranolů jsou tvořeny trojúhelníky a ne rovnoběžníky. Antiprismy se mohou stát velmi složitými.

co je pyramida?

pyramida je polyhedron s polygonovou základnou, která se připojuje k vrcholu (horní bod) s rovnými stranami.

přestože máme tendenci myslet na pyramidy se čtvercovou základnou, jako jsou ty, které postavili starověcí Egypťané, mohou mít ve skutečnosti jakoukoli polygonovou základnu, pravidelnou nebo nepravidelnou. Dále, pyramida může mít vrchol v přímém středu své základny, pravá pyramida, nebo může mít vrchol mimo centrum, když je to šikmá Pyramida.,

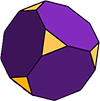
Složitější Polyhedrons

Existuje mnoho více typy mnohostěnů: symetrické a asymetrické, konkávní a konvexní.

například archimedovské pevné látky jsou tvořeny nejméně dvěma různými pravidelnými polygony.

zkrácená kostka (jak je znázorněno) je archimedovská pevná látka se 14 tvářemi. 6 tváří jsou pravidelné osmiúhelníky a dalších 8 jsou pravidelné (rovnostranné) trojúhelníky. Tvar má 36 okrajů a 24 vrcholů (rohů).,

trojrozměrné tvary s křivkami

pevné tvary, které obsahují zakřivený nebo kulatý okraj, nejsou mnohostěny. Polyhedrony mohou mít pouze rovné strany.

mnoho objektů kolem vás bude obsahovat alespoň některé křivky. V geometrii jsou nejčastějšími zakřivenými pevnými látkami válce, kužely, koule a tori (množné číslo pro torus).,

Společné Trojrozměrné Tvary s Křivkami:
Válce	Kužel
Válec má stejný průřez z jednoho konce na druhý. Válce mají dva identické konce buď kruhu nebo oválu. Ačkoli podobné, válce nejsou hranoly jako hranol má (podle definice) rovnoběžník, ploché strany.,	kužel má kruhovou nebo oválnou základnu a vrchol (nebo vrchol). Strana kužele se plynule zužuje k vrcholu. Kužel je podobný pyramidě, ale odlišný jako kužel má jednu zakřivenou stranu a kruhovou základnu.
Koule	Torus
ve Tvaru koule nebo koulí koule je zcela kulatý objekt. Každý bod na povrchu koule je stejná vzdálenost ke středu koule.,	tvarovaný jako prsten, pneumatika nebo kobliha, pravidelný kruhový torus je tvořen otáčením menšího kruhu kolem většího kruhu. Existuje také složitější forma tori.

Plocha

Naše stránky na Výpočet Oblasti, vysvětluje, jak pracovat se oblasti dvojrozměrných tvarech, a musíte pochopit, tyto základy pro výpočet povrchu trojrozměrné tvary.

Pro trojrozměrné tvary mluvíme o ploše povrchu, abychom se vyhnuli záměně.,

své znalosti o oblasti dvourozměrných tvarů můžete použít k výpočtu plochy trojrozměrného tvaru, protože každá tvář nebo strana je účinně dvourozměrný tvar.

proto vypracujete oblast každé tváře a poté je přidáte dohromady.

stejně jako u plochých tvarů je povrchová plocha pevné látky vyjádřena v čtvercových jednotkách: cm2, inches2, m2 a tak dále. Podrobnější informace o měrných jednotkách naleznete na naší stránce systémy měření.,

Příklady na Výpočty Povrchu

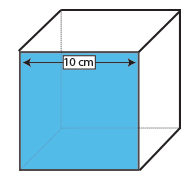
Krychle

povrch krychle je plocha jedné straně (délka x šířka) vynásobí 6, protože všech šest tváře jsou stejné.

vzhledem k tomu, že tvář krychle je čtverec, musíte provést pouze jedno měření – délka a šířka čtverce jsou podle definice stejné.

jedna plocha této krychle je tedy 10 × 10 cm = 100 cm2. Vynásobte 6, počet ploch na krychli a zjistíme, že plocha této krychle je 600cm2.,

Další Pravidelné Polyhedrons

Podobně, plochy jiné pravidelné polyhedrons (platonické pevné látky) lze vyřešit tím, že najde prostor na jedné straně a pak vynásobením odpověď celkový počet stran – viz Základní Polyhedrons diagram výše.

Pokud je plocha jednoho pětiúhelníku tvořící dvanáctistěn je 22cm2 pak to vynásobit celkový počet stran (12) odpovědět 264cm2.,

Pyramida

pro výpočet plochy standardní pyramidy se čtyřmi stejnými trojúhelníkovými stranami a čtvercovou základnou:

nejprve vyřešte plochu základny (čtvercové) délky × šířky.

Další práce na ploše jedné strany (trojúhelník). Změřte šířku podél základny a poté výšku trojúhelníku (také známého jako sklonová délka) od centrálního bodu na základně k vrcholu.,

můžete pak buď rozdělit odpověď do 2, aby vám to plocha jednoho trojúhelníku a pak násobit 4 se dát na povrchu všech čtyř stran, nebo jednoduše vynásobte plochu jednoho trojúhelníku o 2.

nakonec přidejte plochu základny a stran dohromady, abyste našli celkovou plochu pyramidy.

K výpočtu plochy ostatní typy pyramid, přidejte společně plocha základny (tzv. základní oblast) a oblast stranách (boční plochy), možná budete muset měřit stranách individuálně.,

Net diagramy

geometrická síť je dvourozměrný „vzor“ pro trojrozměrný objekt. Sítě mohou být užitečné při zpracování povrchové plochy trojrozměrného objektu. V níže uvedeném diagramu můžete vidět, jak jsou konstruovány základní pyramidy, pokud je pyramida „rozložena“, zůstanete se sítí.

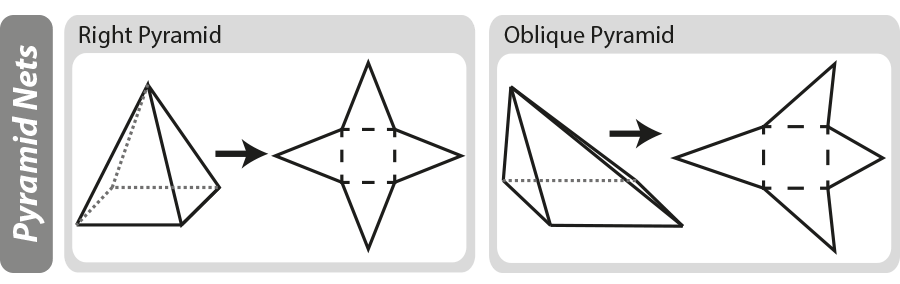
Další informace o síťových diagramech naleznete na naší stránce 3D tvary a sítě.

Prism

Pro výpočet povrchu hranolu:

Hranoly mají dva konce stejné a ploché strany rovnoběžníku.,

Vypočítejte plochu jednoho konce a vynásobte 2.

pro pravidelný hranol (kde jsou všechny strany stejné) Vypočítejte plochu jedné ze stran a vynásobte celkovým počtem stran.

pro nepravidelné hranoly (s různými stranami) Vypočítejte plochu každé strany.

Přidejte své dvě odpovědi dohromady (konce × strany) a najděte celkovou plochu hranolu.,

Válce

Pro výpočet povrchu válce je užitečné přemýšlet o součásti tvaru. Představte si plechovku kukuřice cukrové – má horní a spodní část, z nichž oba jsou kruhy. Pokud jste řezali stranu podél její délky a zploštěli ji, měli byste obdélník. Proto musíte najít oblast dvou kruhů a obdélníku.

nejprve vyřešte oblast jednoho z kruhů.

plocha kruhu je π (pi) × radius2.,

za předpokladu poloměru 5 cm je plocha jednoho z kruhů 3,14 × 52 = 78,5 cm2.

vynásobte odpověď 2, protože existují dva kruhy 157cm2

Plocha strany válce je obvod kruhu × výška válce.

obvod se rovná π X 2 × poloměru. V našem příkladu, 3.14 × 2 × 5 = 31.4

změřte výšku válce-pro tento příklad je výška 10 cm. Povrchová plocha strany je 31,4 × 10 = 314 cm2.,

celková plocha lze nalézt přidáním oblasti, na kruzích a na straně spolu:

157 + 314 = 471cm2

Kužel

Při výpočtu povrchu kužele je třeba použít délku ‚sklon‘, stejně jako poloměr základny.

je však poměrně jednoduché vypočítat:

plocha kruhu na základně kužele je π (pi) × radius2.

v tomto příkladu je součet 3.14 × 52 = 3.14 × 25 = 78.,5cm2

Plocha strany, šikmá část, lze nalézt pomocí tohoto vzorce:

π (pi) × poloměr × délka sklonu.

v našem příkladu je součet 3,14 × 5 × 10 = 157 cm2.

nakonec přidejte základní plochu do boční plochy, abyste získali celkovou plochu kužele.

78.5 + 157 = 235.5cm2

Koule

povrch koule, je relativně jednoduché rozšíření vzorec pro kruh je plocha.

4 × π × radius2.,

pro kouli je často snazší měřit průměr-vzdálenost přes kouli. Pak můžete najít poloměr, který je polovina průměru.

průměr standardního tenisového míče je 2,6 palce. Poloměr je tedy 1,3 palce. Pro vzorec potřebujeme poloměr na druhou. 1.3 × 1.3 = 1.69.

povrchová plocha tenisového míče je proto:

4 × 3,14 × 1,69 = 21,2264 inches2.,

Torus

aby bylo možné vypočítat povrch anuloidu musíte najít dvě hodnoty poloměru.

velký nebo velký poloměr (R) se měří od středu otvoru do středu prstence.

malý nebo menší poloměr (r) se měří od středu prstence k vnějšímu okraji.

diagram zobrazuje dva pohledy na příklad torus a jak měřit jeho radiusy (nebo poloměry).,

výpočet pro nalezení plochy povrchu je ve dvou částech (jeden pro každý poloměr). Výpočet je stejný pro každou část.

vzorec je: surface area = (2nr) (2nr)

pro zpracování povrchové plochy příkladu torus.

(2 × π × R) = (2 × 3.14 × 20) = 125.6

(2 × π × r) = (2 × 3.14 × 4) = 25.12

Vynásobte dvě odpovědi společně najít celkovou plochu například torus.