
krátké vysvětlení a důkaz
Racionální Kořen Věty (RRT) je šikovný nástroj, mít ve svém matematické arsenal. Poskytuje rychlý a špinavý test racionality některých výrazů. A pomáhá najít racionální kořeny polynomů.,
zde je návod, jak a proč to funguje.,e53714″>
Předpokládejme, že máte polynom stupně n s celočíselnými koeficienty:

Racionální Kořen Věta uvádí: je-Li racionální kořen existuje, pak jeho součástí bude dělit na první a poslední koeficienty:

racionální kořen je vyjádřena v nejnižší podmínek., To znamená, že p A q nesdílejí žádné společné faktory. (To bude důležité později.) Čitatel rozděluje konstantu na konci polynomu; demominátor rozděluje přední koeficient.
Jako příklad:
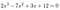
stačí se podívat na 2 a 12.,:
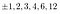
The factors of 2:
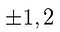
Thus, if a rational root does exist, it’s one of these:
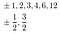
Plug each of these into the polynomial., Which one(s) — if any solve the equation? If none do, there are no rational roots.
Are any cube roots of 2 rational? A rational root, p/q must satisfy this equation.
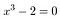
Furthermore:
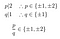
Not one of these candidates qualifies., Skok na:
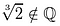
Proč
Jedeme zpět do našeho paradigmatu polynom.,

Scoot the constant to the other side:

Now, plug in our rational root, p/q.,

Vynásobte všechno qⁿ:

Každý výraz na levé straně má p společné. To je fakt.,

Vypadá to horší, než to musí být. Vyměňme všechny ty věci v závorce za s. Je nám úplně jedno, co tam je.
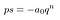
je to mnohem jednodušší na oči.
nezapomeňte, že P A q jsou celá čísla. Také nesdílejí žádné společné faktory., Proto p nemůže rozdělit qⁿ. To se musí rozdělit a₀:
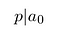
to Znamená, že čitatel rozděluje konstantní výraz.
Nyní, vrátit se k našim paradigma polynom:

Tento čas, špatné první člen na pravé straně.,

Insert the rational root:

As before, multiply by qⁿ.

This time, the common factor on the left is q., Let’s extract it, and lump together the remaining sum as t.
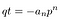
Again, q and p have no common factors. Therefore:
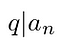
Thus proves the rational root theorem.