Nalezení kvadratických funkcí pro dané paraboly – Kvadratická Funkce

Nalezení Kvadratických Funkcí pro Dané Paraboly

Tam jsou tak mnoho různých typů problémů, můžete být požádáni, s ohledem na kvadratické rovnice. V tomto článku, důraz bude kladen na to, jak můžeme vyvinout kvadratickou rovnici z kvadratického grafu pomocí několika různých metod., Ale než se dostaneme do těchto typů problémů, chvíli si pohrajte s kvadratickými výrazy na této úžasné online grafické kalkulačce zde. Čím pohodlnější jste s kvadratickými grafy a výrazy,tím snazší bude toto téma!

nyní se podívejme na řešení problémů s těmito znalostmi, a to, jak najít rovnici paraboly!

jak najít kvadratickou rovnici z grafu:

Chcete-li najít kvadratickou rovnici z grafu, existují dvě jednoduché metody, které lze použít: pomocí 2 bodů nebo pomocí 3 bodů.,

1) Najděte kvadratickou rovnici od 2 bodů

Chcete-li najít kvadratickou rovnici z grafu pomocí pouze 2 bodů, jeden z těchto bodů musí být vrchol. S vrcholem a jedním dalším bodem můžeme tyto souřadnice rozdělit do toho, co se nazývá „vrcholová forma“, a pak vyřešit naši rovnici., Vrchol vzorec je následující, kde (d,f) je vrchol, bod a (x,y) je další bod

(y±d)=a(x±f)2(y \pm d) = a(x \pm f)^{2}(y±d)=a(x±f)2

Vrchol formulář může také být psán v jeho více „správné“ formě, jako:

y=a(x±f)2∓dy = a(x \pm f)^{2} \mp dy=a(x±f)2∓d

Pomocí tohoto vzorce, všechno, co musíme udělat, je sub na vrchol, a druhý bod, vyřešit, a pak přepsat naše poslední rovnice., Nejlepší způsob, jak se pohodlně používat tento formulář, je udělat s ním příkladný problém.

příklad:

Určete rovnici paraboly zobrazené na obrázku níže.

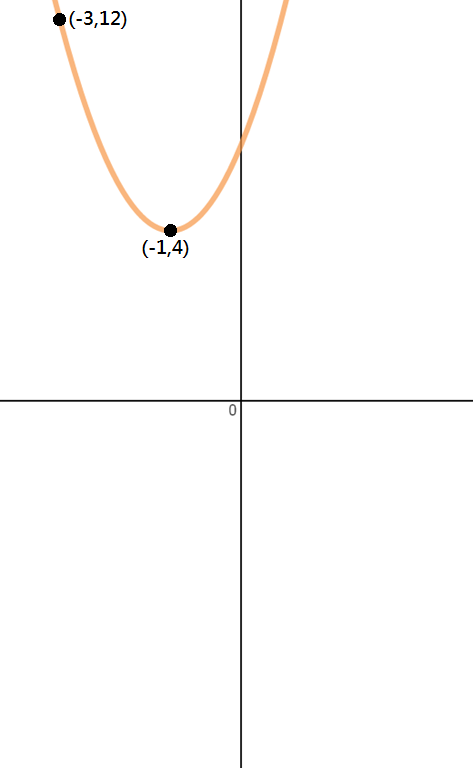
Krok 1: Identifikovat Body,

Od doby, co jsme jsou uvedeny pouze dva body v tomto problém, vertex a další bod, musíme použít vrchol tvoří řešit tuto otázku.,

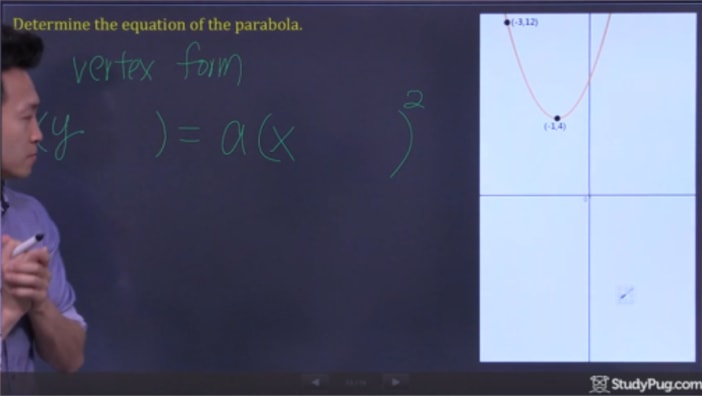
Krok 2: Dílčí Body Do Vrcholu Formy a Řešení pro „a“,

Nyní vše, co musíme udělat, je sub v našich dvou bodů do vertex vzorec a řešení pro „a“ mít všechny informace, psát náš konečný kvadratické rovnice.,4)=(-3+1)2(12 – 4) = a(-3 + 1)^{2}(12-4)=a(-3+1)2

8=(-2)28 = (-2)^{2}8=(-2)2 8=4a8 = 4a8=4a =2a = 2a=2

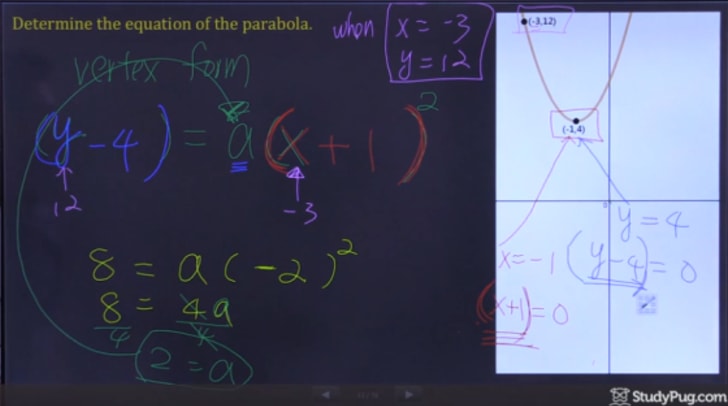
Krok 3: Napište Kvadratickou Rovnici,

Po řešení pro „a“, a nyní máme všechny informace, které potřebujeme vypsat naše konečná odpověď.,

y−4=2(x+1)2y – 4 = 2(x + 1)^{2}y−4=2(x+1)2

A pak, ve správný vrchol formě parabola, naše konečná odpověď je:

y=2(x+1)2+4y = 2(x + 1)^{2} + 4y=2(x+1)2+4

a Že dokončí lekci, na vrcholu formy a jak najít kvadratické rovnice z 2 body!, Pokud si chcete osvěžit paměť na související témata, jako je, jak řešit kvadratické výrazy vrchol v podobě, jak převést pravidelné kvadratické rovnice ze standardní formuláře na vrchol formulář vyplněním náměstí, a jak používat vertex vzorec, ujistěte se, že podívejte se na naše lekce.

2) Najděte kvadratickou rovnici od 3 bodů

v některých případech nebudeme mít takové štěstí, abychom dostali bod na vrcholu. Pokud tomu tak je, nemůžeme již najít kvadratický výraz pomocí pouze dvou bodů a musíme udělat něco trochu jiného., V případě, že jsou uvedeny informace o průsečíky paraboly, stejně jako jeden další bod, můžeme najít kvadratické rovnice pomocí rovnice, která se nazývá „zapracovány formulář“. Obecné rovnice pro započítat formulář vzorec je následující, b a c je souřadnice x hodnot x v bodech:

y=a(x−b)(x−c)y = a(x – b)(x – c)y=a(x−b)(x−c)

Pomocí tohoto vzorce, všechno, co musíme udělat, je sub v x-souřadnice x-zachytí, další bod, a pak vyřešit, takže můžeme napsat naše konečná odpověď., Opět platí, že nejlepší způsob, jak se s touto formou kvadratických rovnic dostat pohodlně, je udělat příkladový problém.

Příklad:

Určete rovnici paraboly je znázorněno na obrázku níže:

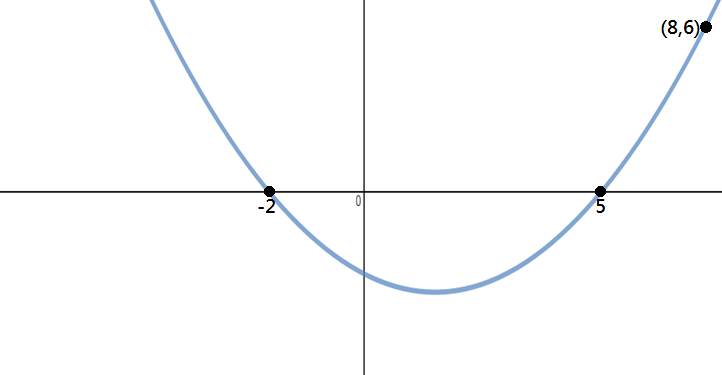
Krok 1: Identifikovat Body,

Od té doby jsme mít tři body v tomto problém, x-zachytí a další bod, můžeme použít zapracovány formou řešit tuto otázku.,

z grafu vidíme, že X-zachytí -2 a 5 a bod na parabole je (8,6).

Krok 2: Dílčí Body Do Vrcholu Formy a Řešení pro „a“,

Nyní vše, co musíme udělat, je sub v naše hodnoty do započítat formulář vzorec a řešení pro „a“ mít všechny informace, psát náš konečný kvadratické rovnice.,(x – 5)y=(x+2)(x−5)

Next, můžeme použít bod na parabole (8,6) řešení pro „a“:

6=a(8+2)(8-5)6 = a(8 + 2)(8 – 5)6=(8+2)(8-5) 6=(10)(3)6 = (10)(3)6=(10)(3) 6=30a6 = 30a6=30a =15a = \frac{1}{5}a=51

Krok 3: Napište Kvadratickou Rovnici,

Po řešení pro „a“, a nyní máme všechny informace, které potřebujeme vypsat naše konečná odpověď.,

y=15(x+2)(x−5)y = \frac{1}{5} (x + 2)(x – 5)y=51(x+2)(x−5)

A to je všechno tam je to! To jsou dvě nejdůležitější metody pro nalezení kvadratické funkce z dané paraboly. Pro další studium do kvadratické funkce a jejich grafy, podívejte se na tyto užitečné videa jednání s diskriminační, grafů kvadratické nerovnice, a kuželoseček.