Bayesova věta najde mnoho použití v teorii pravděpodobnosti a statistice. Existuje mikro šance, že jste nikdy neslyšeli o této větě ve svém životě. Ukázalo se, že tato věta našla svou cestu do světa strojového učení, tvoří jednu z vysoce zdobené algoritmy. V tomto článku se dozvíme vše o naivním Bayesově algoritmu spolu s jeho variacemi pro různé účely ve strojovém učení.
jak jste možná uhodli, to vyžaduje, abychom viděli věci z pravděpodobnostního hlediska., Stejně jako ve strojovém učení máme atributy, proměnné odezvy a předpovědi nebo klasifikace. Pomocí tohoto algoritmu se budeme zabývat distribucí pravděpodobnosti proměnných v datovém souboru a předpovídáme pravděpodobnost proměnné odezvy patřící k určité hodnotě vzhledem k atributům nové instance. Začněme přezkoumáním bayesovy věty.
Bayesova věta
to nám umožňuje prozkoumat pravděpodobnost události na základě předchozí znalosti jakékoli události, která se týkala předchozí události., Takže například pravděpodobnost, že cena domu je vysoká, lze lépe posoudit, pokud známe zařízení kolem něj, ve srovnání s hodnocením provedeným bez znalosti umístění domu. Bayesova věta dělá přesně to.

Výše uvedené rovnice dává základní reprezentace Bayesův teorém., Zde A A B jsou dvě události a
P (A|B) : podmíněná pravděpodobnost , že dojde k události a, vzhledem k tomu, že došlo k b. To je také známé jako zadní pravděpodobnost.
p (a) A P(B): pravděpodobnost a A B bez ohledu na sebe.
P (B / A): podmíněná pravděpodobnost , že dojde k události B, vzhledem k tomu, že došlo k a.
nyní se podívejme, jak to dobře vyhovuje účelu strojového učení.,
Vezměte si jednoduchý problém strojového učení, kde se musíme naučit náš model z dané sady atributů (v příkladech školení) a poté vytvořit hypotézu nebo vztah k proměnné odezvy. Pak použijeme tento vztah k předpovědi odpovědi, vzhledem k atributům nové instance. Pomocí Bayesovy věty je možné vytvořit žáka, který předpovídá pravděpodobnost proměnné odezvy patřící do určité třídy, vzhledem k nové sadě atributů.
zvažte předchozí rovnici znovu. Nyní předpokládejme, že a je proměnná odezvy a B je vstupní atribut., Takže podle rovnice máme
P ( A / B): podmíněná pravděpodobnost proměnné odezvy patřící k určité hodnotě, vzhledem k vstupním atributům. To je také známé jako zadní pravděpodobnost.
P (a): předchozí pravděpodobnost proměnné odezvy.
P (B): pravděpodobnost údajů o školení nebo důkazů.
P(B|A) : toto je známé jako pravděpodobnost údajů o školení.,
Proto, výše uvedené rovnice lze přepsat jako
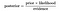
Pojďme se na problém, kde počet atributy, které je rovno n a odezva je logická hodnota, tj. to může být v jedné ze dvou tříd. Také atributy jsou kategorické (2 kategorie pro náš případ). Nyní, abychom vycvičili klasifikátor, budeme muset vypočítat P(B|A) pro všechny hodnoty v instanci a prostoru odezvy., To znamená, že budeme muset vypočítat 2 * (2^n -1), parametry pro učení tohoto modelu. To je ve většině praktických učebních oborů zjevně nereálné. Například, pokud existuje 30 booleovských atributů, pak budeme muset odhadnout více než 3 miliardy parametrů.
naivní Bayesův algoritmus
složitost výše uvedeného bayesovského klasifikátoru musí být snížena, aby byla praktická. Naivní Bayesův algoritmus to dělá tím, že předpokládá podmíněnou nezávislost nad sadou tréninkových dat. To drasticky snižuje složitost výše uvedeného problému na pouhých 2n.,
předpoklad podmíněné nezávislosti států, které, vzhledem k náhodné proměnné X, Y a Z, řekneme, že X je podmíněně nezávislé na Y vzhledem k Z, pokud, a pouze tehdy, pokud rozdělení pravděpodobnosti, kterými se řídí X je nezávislé hodnoty Y vzhledem k Z.
jinými slovy, X a Y jsou podmíněně nezávislé vzhledem k Z, pokud, a pouze pokud, vzhledem k tomu poznání, že se Z vyskytuje, znalosti, zda se X vyskytuje neposkytuje žádné informace o pravděpodobnost, že Y se vyskytující, a poznání, zda se Y vyskytuje neposkytuje žádné informace o pravděpodobnost, že X se vyskytující.,
tento předpoklad činí Bayesův algoritmus naivní.
Vzhledem k tomu, n různé hodnoty atributů, pravděpodobnost, nyní může být zapsáno jako
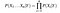
Tady, X představuje atributy, nebo funkce, a Y je závisle proměnná. Nyní, P (X / Y) se rovná produktům, rozdělení pravděpodobnosti každého atributu X dané y.,
maximalizace a Posteriori
to, co nás zajímá, je nalezení zadní pravděpodobnosti nebo P (Y|X). Nyní, pro více hodnot Y, budeme muset vypočítat tento výraz pro každou z nich.
Vzhledem k nové instance Xnew, musíme vypočítat pravděpodobnost, že Y bude mít na daném hodnota, vzhledem k tomu, že pozorované hodnoty atributu z Xnew a vzhledem k tomu, že distribuce P(Y) a P(X|Y) odhad z trénovacích dat.
Jak tedy budeme předpovídat třídu proměnné odezvy na základě různých hodnot, které dosáhneme pro P (Y|X)., Jednoduše vezmeme nejpravděpodobnější nebo maximální z těchto hodnot. Proto je tento postup také známý jako maximalizace a posteriori.
maximalizace pravděpodobnosti
pokud předpokládáme, že proměnná odezvy je rovnoměrně distribuována, to znamená, že je stejně pravděpodobné, že dostaneme jakoukoli odpověď, můžeme algoritmus dále zjednodušit. S tímto předpokladem se priori nebo P (Y) stává konstantní hodnotou, což je 1/Kategorie odpovědi.
As, priori a důkazy jsou nyní nezávislé na proměnné odezvy, tyto mohou být odstraněny z rovnice., Proto je maximalizace posteriori snížena na maximalizaci problému pravděpodobnosti.
distribuce funkcí
jak je vidět výše, musíme odhadnout rozdělení proměnné odezvy ze školicí sady nebo předpokládat rovnoměrné rozdělení. Podobně pro odhad parametrů distribuce funkce je třeba předpokládat distribuci nebo generovat neparametrické modely pro funkce z tréninkové sady. Takové předpoklady jsou známé jako modely událostí. Rozdíly v těchto předpokladech generují různé algoritmy pro různé účely., Pro kontinuální distribuce je gaussovský naivní Bayes algoritmem volby. Pro diskrétní funkce, multinomiální a Bernoulli distribuce jako populární. Podrobná diskuse o těchto variantách je mimo rozsah tohoto článku.
naivní klasifikátory Bayes fungují opravdu dobře ve složitých situacích, navzdory zjednodušeným předpokladům a naivitě. Výhodou těchto klasifikátorů je, že vyžadují malý počet údajů o školení pro odhad parametrů nezbytných pro klasifikaci. Toto je algoritmus volby pro kategorizaci textu., To je základní myšlenka naivních bayesových klasifikátorů, že musíte začít experimentovat s algoritmem.