V Roce 1913 Bohrův model atomu vodíku byl nahrazen Schrodingerʹs vlna mechanický model v roce 1926. Nicméně, Bohrʹs model je stále ziskem učil dnes, protože jeho koncepční a matematické jednoduchosti, a proto zavedla řadu klíčových kvantově mechanické představy, jako jsou kvantová čísla, kvantování pozorovatelné vlastnosti, kvantový skok a stacionární stav.,
Bohr počítá potrubí povolených elektronové energie vyvažování mechanických sil (dostředivá a elektron‐jádro) na elektron vykonávající kruhové dráze o poloměru R o jádro, a pak arbitarily kvantování jeho moment hybnosti. Konečně fiat prohlásil, že elektron byl v non‐vyzařující stacionárním stavu, protože obíhající (zrychluje) náboj vyzařuje energii a zhroutí se do opačně náboj jádra.,
V roce 1924 de Broglie postuloval, vlna‐dualita částečky pro elektron a další masivní částice, čímž poskytuje možnost odstranit některé z arbitariness z Bohrʹs model. Například elektron, který má vlnové vlastnosti, podléhá konstruktivnímu a destruktivnímu rušení. Jak bude ukázáno, vede to přirozeně k kvantizaci elektronové hybnosti a kinetické energie a následně k rozdělování povolených energetických stavů elektronu vzhledem k jádru., Zde prezentovaný model de Broglie-Bohr zachází s elektronem jako s částicí na prstenci s vlnovitými vlastnostmi.
\
de Broglieho hypotéza, že hmota má vlnové vlastnosti.
\
důsledek de Broglieʹs hypotézy; integrální počet vlnových délek se musí vejít do obvodu oběžné dráhy. To představuje kvantové číslo, které může mít hodnoty 1,2,3,… Stav elektronů n = 4 je uveden níže.,
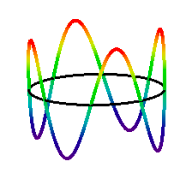
\
Substituce z první rovnice do druhé rovnice vyplývá, že hybnost je quantized.
\
Pokud je hybnost kvantizována, tak je to kinetická energie.
\
což znamená, že celková energie je kvantizována. Druhým termínem je elektrostatická energie elektrostatického potenciálu elektronového protonu.
kvantová mechanická interpretace těchto oběžných drah ʺ je, že se jedná o stacionární stavy. Navzdory skutečnosti, že používáme výraz kinetická energie, což znamená pohyb elektronů, neexistuje žádný pohyb., Elektron zabírá oběžnou dráhu jako částicová vlna, neobíhá kolem jádra. Pokud by obíhala v klasickém smyslu, vyzařovala by energii a rychle se zhroutila do jádra. Je zřejmé, že stabilita hmoty vyžaduje kvantovou mechanickou verzi kinetické energie.
základní stav energie a poloměr oběžné dráze elektronu v atomu vodíku je našel vynesením energii jako funkci orbital radius. Stav země je minimální v celkové energetické křivce., Přirozeně počet lze použít k získání stejných informací minimalizací energie vzhledem k poloměru oběžné dráhy. Grafická metoda má však tu výhodu, že osvětluje otázku atomové stability.
základní konstanty: elektronový náboj, elektronová hmota, Planckova konstanta, permitivita vakua.
kvantové číslo a konverzní fakt mezi metry a pikometry a jouly a attojoules.
\
toto číslo ukazuje, že atomová stabilita zahrnuje rovnováhu mezi potenciálem a kinetickou energií., Elektron je vtažen směrem k jádru atraktivní potenciální energie interakce (~ -1/R), ale je zabráněno kolapsu do jádra extrémně velkou kinetickou energii (~1/R2) spojen s malými drahách.
jak je uvedeno níže, grafický přístup lze také použít k nalezení elektronických vzrušených stavů.
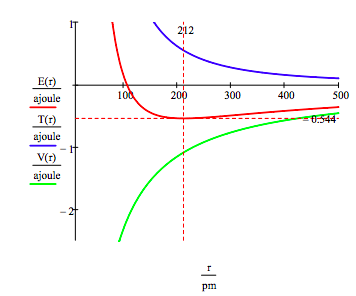
jak již bylo zmíněno výše, rozdělovač povolených elektronových energií lze také získat minimalizací energie vzhledem k poloměru oběžné dráhy. Tento postup přináší