Calculate Log & Antilog Online (Deutsch)

Mathematical Formulas

Calculating log (logbx):

logbx = y implies by = x.,

Wo

• b = base,
• y = Anzahl,
• x = log Wert.

Berechnung Antilog:

y = 10x

Wobei,

• x = anzahl,
• y = antilog wert.

Logarithmen und Anti-Logarithmen: Wie es funktioniert und seine Bedeutung

– Leitfaden verfasst von Corin B. Arenas, veröffentlicht am 1.Oktober 2019

Wenn Sie sich jemals gefragt haben, wie Experten große Entfernungen, Erdbebenintensität und globale Wirtschaftswachstumsraten bestimmen, dann sind Sie hier richtig.

Die Berechnung sehr großer Summen kann langsam und verwirrend sein., Aber mit Hilfe von Logarithmen (log) und Antilogarithmen (Antilog) können Berechnungen einfacher gemacht werden.

Lesen Sie weiter, um mehr über Log und Antilog zu erfahren, wie sie funktionieren und warum dies relevante mathematische Konzepte sind.

Was ist Logarithmus?

Ein Logarithmus ist die Potenz, mit der eine Zahl (als Basis bezeichnet) mit sich selbst multipliziert werden muss, um eine gegebene Zahl zu erhalten. Einfacher ausgedrückt löst der Logarithmus das Problem:

Wie oft multiplizieren wir b, um eine andere Zahl y zu erhalten?,

Logarithmus zählt, wie oft derselbe Faktor multipliziert werden muss, um zu einer bestimmten Zahl zu gelangen.

Wer hat es sich ausgedacht? Jahrhundert vom schottischen Mathematiker, Physiker und Astronomen John Napier als Berechnungswerkzeug erfunden. Er schrieb das Buch Mirifici Logarithmorum Canonis Descriptio mit Tabellen und Zahlen über natürliche Logarithmen und legte die Grundlagen für sein Grundkonzept.

Napier prägte den Begriff Logarithmus aus dem griechischen Wort Logos, was „Verhältnis oder Verhältnis“ bedeutet, und Arithmus, was „Zahl“ bedeutet.,“Wenn es kombiniert wird, bedeutet es wörtlich“ Verhältniszahl.‘

2 Arten von Logarithmen

Der natürliche Logarithmus einer Zahl ist sein Log zur Basis der Konstante e, wobei e ungefähr gleich 2.718281828459 ist. Die Gleichung wird als loge(x) geschrieben.

Wenn ein Logarithmus keine Basis angibt, wie in diesem Beispiel: log(1000), wird er als gemeinsamer Logarithmus bezeichnet, der die Basis 10 verwendet.

log (1000), es ist bekannt als ein gemeinsamer Logarithmus, der die Basis 10 verwendet.

Wie wird Log verwendet?,

Sobald Sie Zahlen von Millionen, Milliarden und Billionen berechnen, kann es ziemlich anstrengend werden. Ob es darum geht, viel Geld zu zählen, das Bevölkerungswachstum oder große Entfernungen zurückzulegen, log kann für Sie arbeiten. Es kann große Summen vereinfachen, die lange und verwirrende Gleichungen beinhalten, wodurch sie leichter zu verstehen sind.

Hier ist die Standardgleichung für log:
logb (x) = y

Wobei

• Die mit sich selbst multiplizierte Zahl (b) die Basis ist.
• Wie oft es multipliziert wird (y), ist der Logarithmus.,
• Die erhaltene Zahl (x) wird in die Klammer geschrieben.

Um zu verstehen, wie das Konzept funktioniert, hier ist ein Beispiel mit einer kleineren Zahl:
Frage: Wie viele 2s multiplizieren wir, um 32 zu erhalten?
b = 2, x = 32

log2(32) = y
Antwort: 2 x 2 x 2 x 2 x 2 = 32

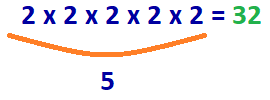
5 Zahl 2 multipliziert werden muss, um die Anzahl der 32.
Die Antwort: log2 (32) = 5

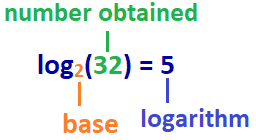
Daher in diesem Beispiel: Der Logarithmus von 32 mit Basis 2 ist 5 oder log Basis 2 von 32 ist 5.,

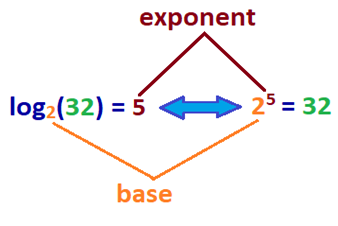
Darüber hinaus ist log die inverse Funktion der Exponentiation, bei der die mathematische Operation als bn geschrieben wird. b ist die Basis, die gemäß der Potenz von n multipliziert wird, dh wie oft sie mit sich selbst multipliziert wird.

Was bedeutet das? Das Protokoll einer Zahl ist der Exponent, mit dem Basis b multipliziert wird, um eine gegebene Zahl zu erhalten. Um Ihnen eine bessere Vorstellung zu geben, beziehen Sie sich auf die Beispielprotokollgleichung, die neben ihrer Exponentialgleichung unten festgelegt ist.,

log	exponent
log2(32) = 5	25 = 32

Versuchen wir es jetzt mit einer großen Anzahl.
Frage: Wie viele 10s multiplizieren wir 150.000.000.000 zu bekommen?
b = 10, x = 150,000,000,000

logb(x) = y
log(150,000,000,000) = y
y = 11.1760912590557
log(150,000,000,000) = 11.,1760912590557

Dies wird durch Verwendung der Protokollfunktion in einem wissenschaftlichen Taschenrechner gelöst. Oder verwenden Sie den Rechner auf dieser Seite um die Antwort zu erhalten.

Wie ist der Numerus im Zusammenhang zu Melden?

Eine Protokollnummer kann dann an ihre ursprüngliche Nummer zurückgegeben werden. Dies kann mit Antilogarithmus (Antilog) erfolgen. Somit ist das Antilog die inverse Funktion von log. Ebenso können Antilog-Funktionen einen vereinfachten Protokollwert exponentiieren.,

Um das Antilog einer Zahl y zu berechnen, müssen Sie die logarithmische Basis b (normalerweise 10, manchmal die Konstante e) auf die Potenz erhöhen, die die Zahl y erzeugt.

Hier ist die Gleichung für Antilog mit Basis 10:
10x = y
Wobei x der Exponent und y der Antilog-Wert ist.

Wenn wir zum Beispiel diese Gleichung log(5) = x, ist ihr Antilog 10x = 5.

• Log: log(5) = 0.698970004336019
• Antilog: 100.698970004336019 = 5

lassen Sie uns Nun versuchen Sie es mit einer größeren Anzahl.,

Wenn wir log(150.000.000.000) = x nehmen, ist sein Antilog 10x = 150.000.000.000.

• Log: log10(150.000.000.000) = 11.1760912590557
• Antilog: 1011.1760912590557= 150.000.000.000

Bedeutung und reale Anwendungen

Vor der Erfindung von Rechnern wurden Logarithmen verwendet, um Berechnungen in verschiedenen Bereichen zu vereinfachen.von wissen, wie navigation, vermessung, astronomie, und später, engineering.

Stellen Sie sich vor, Sie segeln mitten im Nirgendwo im 16., Navigatoren stützten sich damals auf die Position von Sternen und einen Sextantenmechanismus, um ihren genauen Standort zu bestimmen. Ohne moderne Technologie, die Ihnen bei der Berechnung großer Entfernungen hilft, können Sie log verwenden, um Ihre Berechnungen zu vereinfachen. Genauigkeit ist wichtig, oder Sie riskieren mehr Tage auf See mit mageren Vorräten. Weniger Gleichungen bedeuten weniger Raum für Fehler.

Was ist mit anderen praktischen Anwendungen? Live Science besagt, dass Logarithmen geometrische Progressionen mit arithmetischen Progressionen in Beziehung setzen., Wenn Sie jemals sich wiederholende Formen und Muster in Natur, Architektur und Kunst bemerkt haben, besitzen diese Formationen ihre eigenen entsprechenden logarithmischen Werte.

Heute beeinflusst das Wissen, wie diese Muster funktionieren, die Art und Weise, wie die Menschheit Häuser, Gebäude und Stadtlandschaften baut und entwirft.

Logarithmen werden auch verwendet, um das Ausmaß und die Intensität bestimmter Skalen auszudrücken., Abgesehen von großen Entfernungen und hohen Geschwindigkeiten misst es andere Dinge wie:

• Schallintensität
• Schallfrequenz
• Kraft von Stürmen
• Stärke von Erdbeben
• Ätzender Säuregehalt
• Härte von Mineralien
• Helligkeit von Sternen

Nehmen wir als Beispiel Dezibel. Um Lautsprecher um 10 Dezibel lauter zu machen, muss sie um das 10-fache der Leistung versorgt werden. Wenn Sie es auf +20 dB erhöhen, wird es das 100-fache der Leistung benötigen, und um +30 dB wird es 1.000 die Leistung benötigen.

Darüber hinaus schreitet die Schallintensität arithmetisch voran., Es ändert sich auch proportional mit dem Logarithmus einer geometrisch fortschreitenden Schallwelle.

Unten finden Sie eine Tabelle von Live Science, in der verschiedene logarithmische Skalen mit ihren entsprechenden linearen Skalen aufgeführt sind.

In Messraten und Rängen

Laut Kalid Azad, dem Mathematiklehrer dahinter BetterExplained.com Logarithmen sind, wie wir herausfinden, wie schnell etwas wächst.

Allgemeine Logarithmen beschreiben Zahlen grundsätzlich in Bezug auf ihre 10-Potenzen. Wenn es um den Zinssatz geht, ist der Logarithmus das Wachstum einer Investition.,

Bei der Bestimmung der BIP-Wachstumsrate eines Landes überprüfen Analysten das BIP in den folgenden Jahren. Sie nehmen das BIP des Vorjahres und das BIP des folgenden Jahres und berechnen dann den Logarithmus, um die geschätzte Wachstumsrate zu ermitteln.

Suchmaschinen verwenden das Linkdiagramm, um die Wichtigkeit und Vertrauenswürdigkeit von Dokumenten im Web zu bewerten & Autorität. Der PageRank von Google war eine wichtige Weiterentwicklung der Suche, die die Relevanz der Suche erhöhte und Google bei der Markteinführung half.,

Laut Azad ist eine Zielseite mit einem PageRank von 2 auf einer Skala von 1 bis 10 zehnmal beliebter als eine Seite mit einem PageRank von 1. Wenn eine Site einen PageRank von 5 und eine konkurrierende Site einen PageRank von 9 hat, hat sie einen Unterschied von 4 Größenordnungen.

Eine Größenordnung bedeutet ungefähr eine 10-fache Differenz, oder ein Ranking ist 1-stellig größer als das andere. In diesem Fall ist eine Site mit einem PageRank 9 100,000,000 beliebter als eine Site mit PageRank 1.,

Unterm Strich

Log und Antilog sind signifikante Rechenmethoden, mit denen wir große Summen vereinfachen können. Die Vereinfachung verkürzt den Berechnungsprozess und erleichtert das Verständnis von Berechnungen. Dies hilft, Platz für Fehler zu reduzieren.

Darüber hinaus bietet die Verwendung von log messbare Skalen zur Messung von Naturphänomenen wie Erdbebenintensität, Windstärke und Helligkeit von Sternen. In Bezug auf die Finanzen erlauben uns Logarithmen, Zinssätze und Wirtschaftswachstumsraten zu bestimmen.

Es wird praktisch in vielen Bereichen verwendet., Große Werte, die von der Messgenauigkeit abhängen, profitieren von logarithmischen Berechnungen.

Über den Autor

Corin ist ein leidenschaftlicher Forscher und Autor von Finanzthemen—Untersuchung der wirtschaftlichen Trends, wie sie sich auf die Bevölkerung auswirken, sowie wie Verbraucher klügere finanzielle Entscheidungen treffen können. Ihre anderen Feature-Artikel können gelesen werden Inquirer.net und Manileno.com. Sie hat einen Master-Abschluss in kreativem Schreiben von der University of the Philippines, einer der besten akademischen Institutionen der Welt, und einen Bachelor in Kommunikationskunst vom Miriam College.