Das 1913 Bohr-Modell des Wasserstoffatoms wurde 1926 durch Schrodingers wellenmechanisches Modell ersetzt. BohrʹS Modell wird jedoch aufgrund seiner konzeptionellen und mathematischen Einfachheit und weil es eine Reihe wichtiger quantenmechanischer Ideen wie die Quantenzahl, die Quantisierung beobachtbarer Eigenschaften, den Quantensprung und den stationären Zustand einführte, heute noch profitabel gelehrt.,
Bohr berechnete die Verteilung der zulässigen Elektronenenergien, indem er die mechanischen Kräfte (zentripetaler und Elektronenkern) auf einem Elektron ausbalancierte, das eine Kreisbahn mit dem Radius R um den Kern ausführte, und dann seinen Drehimpuls willkürlich quantisierte. Schließlich erklärte er mit Fiat, dass sich das Elektron in einem nicht strahlenden stationären Zustand befinde, da eine umlaufende (beschleunigende) Ladung Energie ausstrahlt und in den entgegengesetzten Ladungskern kollabiert.,
1924 postulierte de Broglie die Wellen-Teilchen-Dualität für das Elektron und andere massive Teilchen und bot damit die Möglichkeit, einen Teil der Arbitarität aus BohrʹS Modell zu entfernen. Zum Beispiel unterliegt ein Elektron, das Welleneigenschaften besitzt, konstruktiven und destruktiven Interferenzen. Wie gezeigt wird, führt dies natürlich zur Quantisierung des Elektronenimpulses und der kinetischen Energie und folglich zu einer Vielzahl zulässiger Energiezustände für das Elektron relativ zum Kern., Das hier vorgestellte de Broglie-Bohr-Modell des Wasserstoffatoms behandelt das Elektron als Teilchen auf einem Ring mit wellenartigen Eigenschaften.
\
de Broglie ‚ s Hypothese, dass die Sache hat wellenartige Eigenschaften.
\
Die Konsequenz von de BrogliʹS Hypothese; Eine integrale Anzahl von Wellenlängen muss in den Umfang der Umlaufbahn passen. Dies führt die Quantenzahl ein, die Werte 1,2,3 haben kann… Der Elektronenzustand n = 4 ist unten dargestellt.,
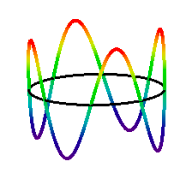
\
Die Substitution der ersten Gleichung in die zweite Gleichung zeigt, dass der Impuls quantisiert wird.
\
Wenn der Impuls quantisiert wird, gilt auch die kinetische Energie.
\
Was bedeutet, dass die Gesamtenergie quantisiert wird. Der zweite Term ist die Elektron-Proton-elektrostatische Potentialenergie.
Die quantenmechanische Interpretation dieserBoBohr-Bahnenʺ ist, dass es sich um stationäre Zustände handelt. Obwohl wir den Ausdruck kinetische Energie verwenden, der Elektronenbewegung impliziert, gibt es keine Bewegung., Das Elektron nimmt die Umlaufbahn als Teilchenwelle ein, es umkreist nicht den Kern. Wenn es im klassischen Sinne umkreist würde, würde es Energie ausstrahlen und schnell in den Kern kollabieren. Offensichtlich erfordert die Stabilität der Materie die quantenmechanische Version der kinetischen Energie.
Die Grundzustandsenergie und der Umlaufbahnradius des Elektrons im Wasserstoffatom werden durch Zeichnen der Energie in Abhängigkeit vom Umlaufbahnradius ermittelt. Der Grundzustand ist das minimum der Gesamtenergie Kurve., Natürlich kann Kalkül verwendet werden, um die gleichen Informationen zu erhalten, indem die Energie in Bezug auf den Umlaufbahnradius minimiert wird. Die grafische Methode hat jedoch die Tugend, das Problem der atomaren Stabilität zu beleuchten.
Grundkonstanten: Elektronenladung, Elektronenmasse, Plancksche Konstante, Vakuumpermitivität.
Quantenzahl und Umwandlungsfaktor zwischen Metern und Pikometern und Joule und Attojoule.
\
\
Diese Abbildung zeigt, dass atomare Stabilität ein Gleichgewicht zwischen potenzieller und kinetischer Energie beinhaltet., Das Elektron wird durch die attraktive potentielle Energieinteraktion (~ -1/R) in Richtung des Kerns gezogen, aber durch die extrem große kinetische Energie (~1/R2), die mit kleinen Bahnen verbunden ist, daran gehindert, in den Kern zu kollabieren.
Wie unten gezeigt, kann der grafische Ansatz auch verwendet werden, um die elektronischen angeregten Zustände zu finden.
\
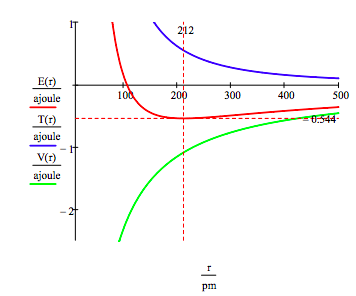
Wie bereits erwähnt, kann die Vielfalt der zulässigen Elektronenenergien auch durch Minimierung der Energie in Bezug auf den Umlaufbahnradius erhalten werden. Dieses Verfahren ergibt,